Estadística Correlacional

## Asociación, inferencia y reporte

----
.pull-left[

## Juan Carlos Castillo
## Sociología FACSO - UChile
## 2do Sem 2023 
## [.orange[correlacional.netlify.com]](https:/correlacional.netlify.com)
]

.pull-right-narrow[
.center[
.content-block-gray[
## Sesión 4: 
## .orange[Tamaños de efecto, otros coeficientes y matrices]]
]
]
---

---
class: roja

## Objetivos de la sesión de hoy

### 1. Calcular e interpretar el coeficiente de determinación

### 2. Aprender a interpretar los tamaños de efecto del coeficiente de correlación

### 3. Conocer, calcular e interpretar coeficientes de correlación alternativos para datos ordinales

### 4. Reportar e interpretar matrices de correlación

---
class: middle center

# Lectura: Field 205-244 Correlation

---
class: roja right

# .black[Contenidos]

### .yellow[1- Resumen sesión anterior]

### 2- Magnitud de la correlación

### 3- Otros coeficientes de correlación

### 4- Matrices de correlación

]

---

## Hacia la covarianza

.pull-left[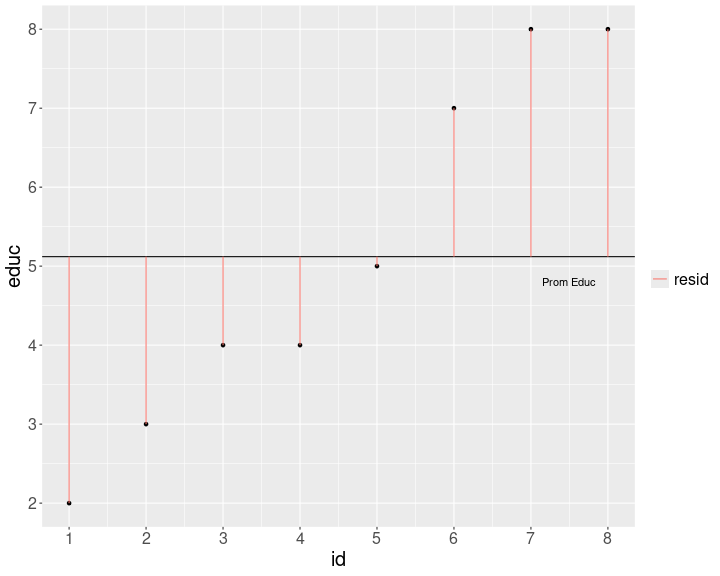
![](04_corr-extensiones_files/figure-html/unnamed-chunk-2-1.png)
.center[
### Educación
]

]
.pull-right[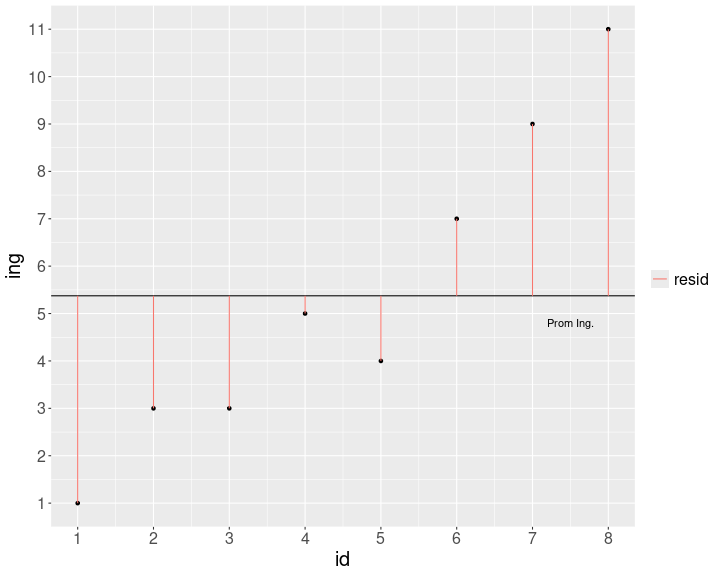
![](04_corr-extensiones_files/figure-html/unnamed-chunk-3-1.png)
.center[
### Ingreso
]

]

---
# Covarianza

`$$\sigma_{edu}^{2}={\sum_{i=1}^{N}(x_{i}-\bar{x})^{2}\over {N - 1}}$$`
`$$\sigma_{edu}^{2}={\sum_{i=1}^{N}(x_{i}-\bar{x})(x_{i}-\bar{x})\over {N - 1}}$$`

]

]
.pull-right[

`$$\sigma_{ing}^{2}={\sum_{i=1}^{N}(y_{i}-\bar{y})^{2}\over {N - 1}}$$`
`$$\sigma_{ing}^{2}={\sum_{i=1}^{N}(y_{i}-\bar{y})(y_{i}-\bar{y})\over {N - 1}}$$`

]

--
.content-box-red[
`$$Covarianza=cov(x,y) = \frac{\sum_{i=1}^{N}(x_i - \bar{x})(y_i - \bar{y})} {N-1}$$`
]

---
## Cálculo correlación

.pull-left[
.small[
<div style="border: 1px solid #ddd; padding: 0px; overflow-y: scroll; height:450px; overflow-x: scroll; width:500px; "><table>
 <thead>
  <tr>
   <th style="text-align:right;position: sticky; top:0; background-color: #FFFFFF;"> educ </th>
   <th style="text-align:right;position: sticky; top:0; background-color: #FFFFFF;"> ing </th>
   <th style="text-align:right;position: sticky; top:0; background-color: #FFFFFF;"> dif_m_educ2 </th>
   <th style="text-align:right;position: sticky; top:0; background-color: #FFFFFF;"> dif_m_ing2 </th>
   <th style="text-align:right;position: sticky; top:0; background-color: #FFFFFF;"> dif_xy </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 2 </td>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 9.77 </td>
   <td style="text-align:right;"> 19.14 </td>
   <td style="text-align:right;"> 13.67 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 3 </td>
   <td style="text-align:right;"> 3 </td>
   <td style="text-align:right;"> 4.52 </td>
   <td style="text-align:right;"> 5.64 </td>
   <td style="text-align:right;"> 5.05 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 4 </td>
   <td style="text-align:right;"> 3 </td>
   <td style="text-align:right;"> 1.27 </td>
   <td style="text-align:right;"> 5.64 </td>
   <td style="text-align:right;"> 2.67 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 4 </td>
   <td style="text-align:right;"> 5 </td>
   <td style="text-align:right;"> 1.27 </td>
   <td style="text-align:right;"> 0.14 </td>
   <td style="text-align:right;"> 0.42 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 5 </td>
   <td style="text-align:right;"> 4 </td>
   <td style="text-align:right;"> 0.02 </td>
   <td style="text-align:right;"> 1.89 </td>
   <td style="text-align:right;"> 0.17 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 7 </td>
   <td style="text-align:right;"> 7 </td>
   <td style="text-align:right;"> 3.52 </td>
   <td style="text-align:right;"> 2.64 </td>
   <td style="text-align:right;"> 3.05 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 8 </td>
   <td style="text-align:right;"> 9 </td>
   <td style="text-align:right;"> 8.27 </td>
   <td style="text-align:right;"> 13.14 </td>
   <td style="text-align:right;"> 10.42 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 8 </td>
   <td style="text-align:right;"> 11 </td>
   <td style="text-align:right;"> 8.27 </td>
   <td style="text-align:right;"> 31.64 </td>
   <td style="text-align:right;"> 16.17 </td>
  </tr>
</tbody>
</table></div>

]
]

.pull-right[
`$$r=\frac{\sum(x-\bar{x})(y-\bar{y})}{\sqrt{\sum(x-\bar{x})^{2} \sum(y-\bar{y})^{2}}}$$`

``` r
sum(data$dif_xy); sum(data$dif_m_educ2);sum(data$dif_m_ing2)
```

```
[1] 51.625
```

```
[1] 36.875
```

```
[1] 79.875
```

]

---

## Cálculo correlación
.pull-left[

`\begin{align*}
r &= \frac{\sum(x-\bar{x})(y-\bar{y})}{\sqrt{\sum(x-\bar{x})^{2} \sum(y-\bar{y})^{2}}} \\ \\
&= \frac{51.625}{ \sqrt{36.875*79.875}} \\ \\
&= \frac{51.625}{54.271} \\ \\
&= 0.951
\end{align*}`

]

``` r
cor(data$educ,data$ing)
```

```
[1] 0.9512367
```
]

---
# Nubes de puntos (scatterplot)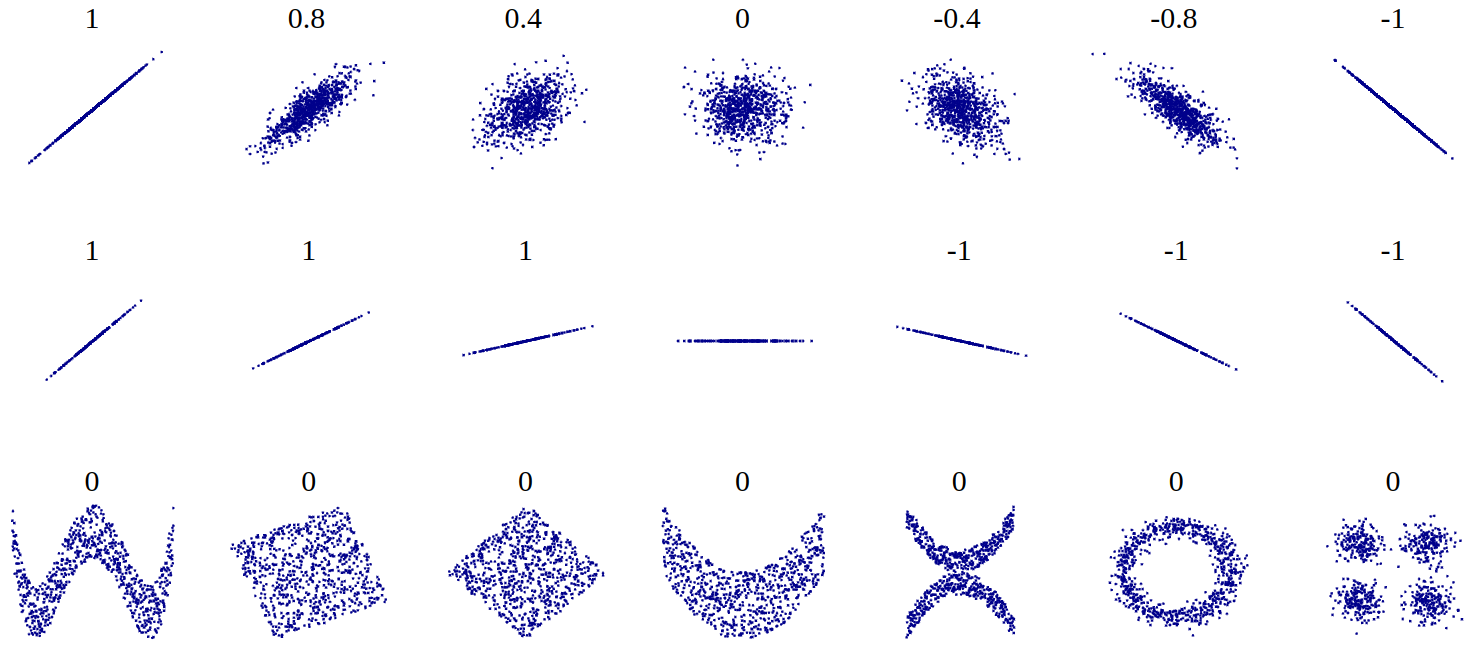

## Interpretación

- El coeficiente de correlación (de Pearson) es una medida de asociación lineal entre variables, que indica el sentido y la fuerza de la asociación

- Varía entre +1 y -1, donde

- valores .black[positivos] indican relación directa (aumenta una, aumenta la otra)
  
  - valores .black[negativos] indican relación inversa (aumenta una, disminuye la otra)

---
class: roja right

# .black[Contenidos]

### 1- Resumen sesión anterior

### .yellow[2- Magnitud de la correlación]

### 3- Otros coeficientes de correlación

### 4- Matrices de correlación

]

---
.pull-left[

Si dos variables covarían, entonces .red[comparten varianza]
![](img/ingresoeduc.png)

]

<br>
<br>
# .red[¿Cuánta varianza comparten?

]
]
---
# Estableciendo la varianza compartida

La varianza compartida puede pensarse como 1 - la varianza no compartida (o varianza única)

La varianza no compartida se asocia al concepto de .red[residuos], es decir, la cantidad de varianza que no está contenida en la correlación

]

.pull-right[
![](https://multivariada.netlify.app/slides/04-regsimple2/residuals.png)
]
---
# Estableciendo la varianza compartida
.pull-left[
Para poder obtener los residuos vamos a generar una .red[recta] que represente la asociación entre las variables. Esta es la recta de **regresión** <sup>1</sup>

Esta recta nos permite obtener un valor estimado de `$y$` para cada valor de `$x$`
<br>
<br>
<br>
<br>
<br>
<br>
<br>
<br>
<br>
.small[[1] Detalles próximo semestre]
]

![](04_corr-extensiones_files/figure-html/unnamed-chunk-7-1.png)

]

---
.pull-left[
.small[

``` r
reg1 <- lm(ing ~ educ, data=data)
data$predict <-predict.lm(reg1)

plot2 <-ggplot(data, 
  aes(x=educ, y=predict)) + 
  geom_point(
    colour = "red", 
    size = 5) +
  theme(text = 
    element_text(size = 20))+
  stat_smooth(method = "lm", 
    se = FALSE, fullrange = T)
```
]
]
.pull-right[
.small[

``` r
plot2
```

![](04_corr-extensiones_files/figure-html/unnamed-chunk-9-1.png)
]

]

---

`\begin{align*}
SS_{tot}&=SS_{reg} + SS_{error} \\ 
\Sigma(y_i - \bar{y})^2&=\Sigma (\hat{y}_i-\bar{y})^2 +\Sigma(y_i-\hat{y}_i)^2
\end{align*}`

---
# Varianza compartida

`$$SS_{tot}=SS_{reg} + SS_{error}$$`

`$$\frac{SS_{tot}}{SS_{tot}}=\frac{SS_{reg}}{SS_{tot}} + \frac{SS_{error}}{SS_{tot}}$$`

`$$1=\frac{SS_{reg}}{SS_{tot}}+\frac{SS_{error}}{SS_{tot}}$$`

`$$\frac{SS_{reg}}{SS_{tot}}= 1- \frac{SS_{error}}{SS_{tot}}=R^2$$`

---
# ¿Qué relación tienen `$R^2$` y `$r$` (correlación)?

Por lo tanto, en nuestro ejemplo:
.small[

``` r
cor(data$educ,data$ing)
```

```
[1] 0.9512367
```
]
`\begin{align*}
r&= 0.95 \\
r^2&=0.95 ^2 \\
r^2&=0.902 = R^2
\end{align*}`

]
--

_El porcentaje de varianza compartida entre educación e ingreso es de 90%._

_Es decir, ambas variables comparten el 90% de su varianza_
]]
---
# `$R^2$` o coeficiente de determinación

- ¿Cuánto de los ingresos se asocia a educación, y viceversa?

- el `$R^2$`
  - es la proporción de la varianza de Y que se asocia a X
  
  - varía entre 0 y 1, y usualmente se expresa en porcentaje

---
# Criterios de Cohen para tamaños de efecto

- El coeficiente de correlación `$r$` de Pearson nos indica la dirección y la fuerza/intensidad de la asociación.

- Pero, ¿qué nos dice el tamaño del coeficiente? Por ejemplo, si el coeficiente es 0.5, ¿esto es pequeño, mediano o grande?

- Cohen (1988, 1992) sugiere una serie de criterios convencionales para clasificar efectos como pequeños, medianos o grandes.

---
class: center
![:scale 75%](img/cohen.png)
---
class: middle

## Para el caso de correlación de Pearson, Cohen sugiere:

- tamaño de efecto .roja[pequeño]: alrededor de .red[0.10]

- tamaño de efecto .roja[mediano]: alrededor de .red[0.30]

- tamaño de efecto .roja[grande]: alrededor de .red[0.50] y más

---
# Resumen

- **Coeficiente de determinación** `$R^2$`: varianza compartida entre variables

- **Tamaño de efecto:** valores convencionales para establecer si una magnitud es pequeña, mediana o grande.

- Varianza compartida y tamaño de efecto son relevantes de reportar junto a la información de inferencia y significación estadística (próxima unidad)

---
class: roja right

# .black[Contenidos]

### 1- Resumen sesión anterior

### 2- Magnitud de la correlación

### .yellow[3- Otros coeficientes de correlación]

### 4- Matrices de correlación

]

---
# Coeficiente de correlación de Spearman

- se utiliza para variables ordinales y/o cuando se se violan supuestos de distribución normal
  
  - es equivalente a la correlación de Pearson del ranking de las observaciones analizadas 
  
  - es alta cuando las observaciones tienen un ranking similar

---
# Cálculo Spearman

- se le asigna un número de ranking a cada valor

- el valor más bajo obtiene el mayor ranking, y el más alto el menor

- en caso de valores repetidos se produce un "empate", y entonces el ranking se promedia.

---
# Ejemplo: variable Educación

``` r
data$educ
```

```
[1] 2 3 4 4 5 7 8 8
```

Como estos valores están ordenados de menor a mayor, entonces en principio los valores de ranking serían:

`8 7 6 5 4 3 2 1`.
]

Pero, hay un par de empates

- el valor 4 está repetido y corresponden a los ranking 6 y 5, por lo tanto a ambos se les asigna el promedio de estos rankings: 5,5

- lo mismo sucede con el valor 8 en los rankings 2 y 1, por lo tanto a ambos se les asigna el valor 1,5 ]

]

---

``` r
*data
```
]
 
.panel2-spearman-auto[

```
  id educ ing mean_educ dif_m_educ dif_m_educ2 mean_ing dif_m_ing dif_m_ing2
1  1    2   1     5.125     -3.125    9.765625    5.375    -4.375  19.140625
2  2    3   3     5.125     -2.125    4.515625    5.375    -2.375   5.640625
3  3    4   3     5.125     -1.125    1.265625    5.375    -2.375   5.640625
4  4    4   5     5.125     -1.125    1.265625    5.375    -0.375   0.140625
5  5    5   4     5.125     -0.125    0.015625    5.375    -1.375   1.890625
6  6    7   7     5.125      1.875    3.515625    5.375     1.625   2.640625
7  7    8   9     5.125      2.875    8.265625    5.375     3.625  13.140625
8  8    8  11     5.125      2.875    8.265625    5.375     5.625  31.640625
     dif_xy predict
1 13.671875     1.0
2  5.046875     2.4
3  2.671875     3.8
4  0.421875     3.8
5  0.171875     5.2
6  3.046875     8.0
7 10.421875     9.4
8 16.171875     9.4
```
]

---
count: false

``` r
data %>%
* select (educ, ing)
```
]
 
.panel2-spearman-auto[

```
  educ ing
1    2   1
2    3   3
3    4   3
4    4   5
5    5   4
6    7   7
7    8   9
8    8  11
```
]

---
count: false

``` r
data %>%
  select (educ, ing) %>%
* mutate(., educ_rank=c(8,7,5.5,5.5,4,3,1.5,1.5))
```
]
 
.panel2-spearman-auto[

```
  educ ing educ_rank
1    2   1       8.0
2    3   3       7.0
3    4   3       5.5
4    4   5       5.5
5    5   4       4.0
6    7   7       3.0
7    8   9       1.5
8    8  11       1.5
```
]

---
count: false

``` r
data %>%
  select (educ, ing) %>%
  mutate(., educ_rank=c(8,7,5.5,5.5,4,3,1.5,1.5)) %>%
* mutate(., ing_rank=c(8,6.5,6.5,4,5,3,2,1))
```
]
 
.panel2-spearman-auto[

```
  educ ing educ_rank ing_rank
1    2   1       8.0      8.0
2    3   3       7.0      6.5
3    4   3       5.5      6.5
4    4   5       5.5      4.0
5    5   4       4.0      5.0
6    7   7       3.0      3.0
7    8   9       1.5      2.0
8    8  11       1.5      1.0
```
]

---
count: false

``` r
data %>%
  select (educ, ing) %>%
  mutate(., educ_rank=c(8,7,5.5,5.5,4,3,1.5,1.5)) %>%
  mutate(., ing_rank=c(8,6.5,6.5,4,5,3,2,1))

*cor(data_spr$educ_rank, data_spr$ing_rank)
```
]
 
.panel2-spearman-auto[

```
  educ ing educ_rank ing_rank
1    2   1       8.0      8.0
2    3   3       7.0      6.5
3    4   3       5.5      6.5
4    4   5       5.5      4.0
5    5   4       4.0      5.0
6    7   7       3.0      3.0
7    8   9       1.5      2.0
8    8  11       1.5      1.0
```

```
[1] 0.9394112
```
]

---
Cálculo directo en `R`:

``` r
cor.test(data$educ, data$ing, "two.sided", "spearman")
```

```

Spearman's rank correlation rho

data:  data$educ and data$ing
S = 5.0895, p-value = 0.0005311
alternative hypothesis: true rho is not equal to 0
sample estimates:
      rho 
0.9394112 
```

---
# Coeficiente de correlación Tau de Kendall

.pull-left[
- Recomendado cuando hay un set de datos pequeños y/o cuando hay mucha repetición de observaciones en el mismo ranking

- Se basa en una comparación de pares de observaciones concordantes y discordantes

]

En `R`:

``` r
cor.test(data$educ, data$ing,
         "two.sided", 
         "kendall")
```

```

Kendall's rank correlation tau

data:  data$educ and data$ing
z = 2.9115, p-value = 0.003597
alternative hypothesis: true tau is not equal to 0
sample estimates:
      tau 
0.8680791 
```
]
]

---
class: inverse 
## Recomendaciones generales

- Pearson es el coeficiente de correlación por defecto

- En caso de datos en escala de medición ordinal se puede aplicar Spearman (aunque Pearson es también aceptado en este contexto).

- Kendall se reporta en casos muy específicos donde hay un set de datos pequeños y repetición de observaciones en el mismo ranking ("empates")

---
class: roja right

# .black[Contenidos]

### 1- Resumen sesión anterior

### 2- Magnitud de la correlación

### 3- Otros coeficientes de correlación

### .yellow[4- Matrices de correlación]

]

---
# Matriz de correlación

- una matriz de correlación se conforma cuando se representa simultaneamente más de un par de asociaciones bivariadas

- por ejemplo, si agregamos la variable edad a nuestra base de datos:

``` r
data$edad <- c(50, 65, 27, 15, 40, 22, 25, 38)
```

Tenemos .red[3 variables], y por lo tanto los siguentes pares de correlaciones posibles: ingreso-educación, ingreso-edad, y educación-edad

---

``` r
*cor_mat <- data
```
]
 
.panel2-matriz1-auto[

]

---
count: false

``` r
cor_mat <- data %>%
* select(educ, ing, edad)
```
]
 
.panel2-matriz1-auto[

]

---
count: false

``` r
cor_mat <- data %>%
  select(educ, ing, edad)   %>%
* cor(.)
```
]
 
.panel2-matriz1-auto[

]

---
count: false

``` r
cor_mat <- data %>%
  select(educ, ing, edad)   %>%
  cor(.)
*cor_mat
```
]
 
.panel2-matriz1-auto[

```
           educ        ing       edad
educ  1.0000000  0.9512367 -0.4704649
ing   0.9512367  1.0000000 -0.4058455
edad -0.4704649 -0.4058455  1.0000000
```
]

---
count: false

``` r
cor_mat <- data %>%
  select(educ, ing, edad)   %>%
  cor(.)
cor_mat
*round(cor_mat, 3)
```
]
 
.panel2-matriz1-auto[

```
           educ        ing       edad
educ  1.0000000  0.9512367 -0.4704649
ing   0.9512367  1.0000000 -0.4058455
edad -0.4704649 -0.4058455  1.0000000
```

```
       educ    ing   edad
educ  1.000  0.951 -0.470
ing   0.951  1.000 -0.406
edad -0.470 -0.406  1.000
```
]

---
count: false

``` r
cor_mat <- data %>%
  select(educ, ing, edad)   %>%
  cor(.)
cor_mat
round(cor_mat, 3)
*sjPlot::tab_corr(cor_mat)
```
]
 
.panel2-matriz1-auto[

```
           educ        ing       edad
educ  1.0000000  0.9512367 -0.4704649
ing   0.9512367  1.0000000 -0.4058455
edad -0.4704649 -0.4058455  1.0000000
```

```
       educ    ing   edad
educ  1.000  0.951 -0.470
ing   0.951  1.000 -0.406
edad -0.470 -0.406  1.000
```

<table style="border-collapse:collapse; border:none;">
<tr>
<th style="font-style:italic; font-weight:normal; border-top:double black; border-bottom:1px solid black; padding:0.2cm;">&nbsp;</th>
<th style="font-style:italic; font-weight:normal; border-top:double black; border-bottom:1px solid black; padding:0.2cm;">educ</th>
<th style="font-style:italic; font-weight:normal; border-top:double black; border-bottom:1px solid black; padding:0.2cm;">ing</th>
<th style="font-style:italic; font-weight:normal; border-top:double black; border-bottom:1px solid black; padding:0.2cm;">edad</th>
</tr>
<tr>
<td style="font-style:italic;">educ</td>
<td style="padding:0.2cm; text-align:center;">&nbsp;</td>
<td style="padding:0.2cm; text-align:center;">0.951</td>
<td style="padding:0.2cm; text-align:center;">-0.470</td>
</tr>
<tr>
<td style="font-style:italic;">ing</td>
<td style="padding:0.2cm; text-align:center;">0.951</td>
<td style="padding:0.2cm; text-align:center;">&nbsp;</td>
<td style="padding:0.2cm; text-align:center;">-0.406</td>
</tr>
<tr>
<td style="font-style:italic;">edad</td>
<td style="padding:0.2cm; text-align:center;">-0.470</td>
<td style="padding:0.2cm; text-align:center;">-0.406</td>
<td style="padding:0.2cm; text-align:center;">&nbsp;</td>
</tr>
<tr>
<td colspan="4" style="border-bottom:double black; border-top:1px solid black; font-style:italic; font-size:0.9em; text-align:right;">Computed correlation used pearson-method with listwise-deletion.</td>
</tr>
 
</table>
]

---
# Matriz de correlaciones

- tabla de doble entrada donde las variables se presentan tanto en las filas como en las columnas

- el coeficiente de correlación correspondiente al par de variables aparece en la intersección de las columnas

- existe información redundante

- las correlaciones se repiten, dado que las variables se intersectan dos veces en la tabla
  - la diagonal tiene solo unos (1), ya que es la correlación de la variable consigo misma

---

``` r
*sjPlot::tab_corr(cor_mat,
* triangle = "lower",
* title = "Tabla de correlaciones del ejemplo"
* )
```
]
 
.panel2-matriz2-auto[
<table style="border-collapse:collapse; border:none;">
<caption style="font-weight: bold; text-align:left;">Tabla de correlaciones del ejemplo</caption>
<tr>
<th style="font-style:italic; font-weight:normal; border-top:double black; border-bottom:1px solid black; padding:0.2cm;">&nbsp;</th>
<th style="font-style:italic; font-weight:normal; border-top:double black; border-bottom:1px solid black; padding:0.2cm;">educ</th>
<th style="font-style:italic; font-weight:normal; border-top:double black; border-bottom:1px solid black; padding:0.2cm;">ing</th>
<th style="font-style:italic; font-weight:normal; border-top:double black; border-bottom:1px solid black; padding:0.2cm;">edad</th>
</tr>
<tr>
<td style="font-style:italic;">educ</td>
<td style="padding:0.2cm; text-align:center;">&nbsp;</td>
<td style="padding:0.2cm; text-align:center;">&nbsp;</td>
<td style="padding:0.2cm; text-align:center;">&nbsp;</td>
</tr>
<tr>
<td style="font-style:italic;">ing</td>
<td style="padding:0.2cm; text-align:center;">0.951</td>
<td style="padding:0.2cm; text-align:center;">&nbsp;</td>
<td style="padding:0.2cm; text-align:center;">&nbsp;</td>
</tr>
<tr>
<td style="font-style:italic;">edad</td>
<td style="padding:0.2cm; text-align:center;">-0.470</td>
<td style="padding:0.2cm; text-align:center;">-0.406</td>
<td style="padding:0.2cm; text-align:center;">&nbsp;</td>
</tr>
<tr>
<td colspan="4" style="border-bottom:double black; border-top:1px solid black; font-style:italic; font-size:0.9em; text-align:right;">Computed correlation used pearson-method with listwise-deletion.</td>
</tr>
 
</table>
]

---

``` r
*library(corrplot)
```
]
 
.panel2-matriz3-auto[

]

---
count: false
 
# Matriz con librería  corrplot
.panel1-matriz3-auto[

``` r
library(corrplot)
*corrplot(cor_mat)
```
]
 
.panel2-matriz3-auto[
![](04_corr-extensiones_files/figure-html/matriz3_auto_02_output-1.png)
]

---

``` r
*corrplot(cor_mat,
* method = 'number')
```
]
 
.panel2-matriz31-auto[
![](04_corr-extensiones_files/figure-html/matriz31_auto_01_output-1.png)
]

---

``` r
*corrplot(cor_mat,
* method = 'number',
* type = 'lower',
* number.cex = 3,
* tl.cex = 3,
* diag = FALSE)
```
]
 
.panel2-matriz4-auto[
![](04_corr-extensiones_files/figure-html/matriz4_auto_01_output-1.png)
]

---

``` r
*corrplot.mixed(cor_mat,
* lower = "number",
* upper = "circle",
* number.cex = 3,
* tl.cex = 3,
* diag = "n")
```
]
 
.panel2-matriz5-auto[
![](04_corr-extensiones_files/figure-html/matriz5_auto_01_output-1.png)
]

---

``` r
*corrplot(cor_mat,
* type = "lower",
* addCoef.col = 'white',
* number.cex = 3,
* tl.cex = 3,
* diag = FALSE)
```
]
 
.panel2-matriz6-auto[
![](04_corr-extensiones_files/figure-html/matriz6_auto_01_output-1.png)
]

---

``` r
*corrplot(cor_mat,
* type = "lower",
* addCoef.col = 'white',
* number.cex = 3,
* tl.cex = 3,
* diag = FALSE,
* method = 'square')
```
]
 
.panel2-matriz7-auto[
![](04_corr-extensiones_files/figure-html/matriz7_auto_01_output-1.png)
]

---
# Consideraciones sobre casos perdidos

- Cuando hay casos perdidos en las variables, ¿cuál es el número de casos de la matriz de correlaciones?

- Las correlaciones bivariadas se calculan con información completa, por lo tanto si hay un dato perdido en una de las variables se elimina el caso completo

- Algunas funciones lo hacen de manera automática, en otras hay que especificarlo previamente

---
# Ejemplo

Agreguemos un caso perdido (NA en R) a una de nuestras variables

``` r
data$edad
```

```
[1] 50 65 27 15 40 22 25 38
```

``` r
data$edad <-replace(data$edad, data$edad==15, NA)
data$edad
```

```
[1] 50 65 27 NA 40 22 25 38
```

---
.medium[

``` r
cormat_NA <- data %>% select(educ, ing, edad) %>% cor(.)
round(cormat_NA,3)
```

```
      educ   ing edad
educ 1.000 0.951   NA
ing  0.951 1.000   NA
edad    NA    NA    1
```

``` r
cormat_listwise <- data %>% select(educ, ing, edad) %>% 
  cor(., use = "complete.obs")
round(cormat_listwise, 3)
```

```
       educ    ing   edad
educ  1.000  0.962 -0.669
ing   0.962  1.000 -0.494
edad -0.669 -0.494  1.000
```
]

---
# Eliminación de casos perdidos por lista (o listwise)

- las correlaciones bivariadas requieren eliminación de casos perdidos tipo listwise, es decir, si hay un dato perdido en una variable se pierde el caso completo

- Para conocer el número de casos con que se calculó la matriz:

``` r
sum(complete.cases(data))
```

```
[1] 7
```
]

Por lo tanto, en el cálculo se perdió el caso o fila completa de la base (de 8 casos) que tenía el caso perdido.

---
# Eliminación de casos perdidos por pares (o pairwise)

- en el caso de las matrices de correlaciones es posible tomar la opción .red[pairwise] para casos perdidos

- pairwise quiere decir que se eliminan los casos perdidos solo cuando afectan al cálculo de un par específico.

- en el caso de nuestro ejemplo, si consideramos listwise todas las correlaciones tienen 7 casos, pero con pairwise la correlación entre educación e ingreso mantendría 8 casos.

- por lo tanto, pairwise permite mayor rescate de información y mayor N en el cálculo de matrices de correlaciones

---
# Opción pairwise en correlación en R

``` r
data %>% select(educ, ing, edad) %>% 
  cor(., use = "pairwise")
```

```
           educ        ing       edad
educ  1.0000000  0.9512367 -0.6693607
ing   0.9512367  1.0000000 -0.4941732
edad -0.6693607 -0.4941732  1.0000000
```
En este caso vemos una leve variación en el coeficiente comprometido (educ-ing) comparando listwise con pairwise

---
# Número de casos pairwise

``` r
data %>% select(educ,ing,edad) %>% psych::pairwiseCount() 
```

```
     educ ing edad
educ    8   8    7
ing     8   8    7
edad    7   7    7
```
Se indica que en las correlaciones con edad se utilizaron 7 casos, mientras en la correlación entre ingreso y educación se utilizan 8 casos con el método pairwise

---
class: inverse
## Resumen

.medium[
- Reporte de correlación: además de reportar la intensidad y el sentido, acompañar reporte de tamaño de efecto y varianza compartida `$R^2$`

- Correlación de Spearman: apropiada para variables ordinales, equivale a la correlación de Pearson del ranking de las variables

- Matriz de correlaciones: forma tradicional de reporte de asociaciones de las variables de una investigación, importante considerar tratamiento de datos perdidos (listwise o pairwise)
]

---

# ASISTENCIA

![:scale 90%](img/qr-correlacional-asistencia.png)
]

## Asociación, inferencia y reporte

----
.pull-left[

## Juan Carlos Castillo
## Sociología FACSO - UChile
## 2do Sem 2023 
## [.orange[correlacional.netlify.com]](https://encuestas-sociales.netlify.com)
]