+ - 0:00:00
Notes for current slide
Notes for next slide

Estadística Correlacional

Asociación, inferencia y reporte

Juan Carlos Castillo

Sociología FACSO - UChile

2do Sem 2023

correlacional.netlify.com

Sesión 5:

Introducción a la Inferencia Estadística

1 / 50

Contenidos

1- Resumen sesión anterior

2- Inferencia y muestras

3- Aleatoridad y probabilidad

4- Curva normal y puntajes Z

2 / 50

Resumen

  • Reporte de correlación: además de reportar la intensidad y el sentido, acompañar reporte de tamaño de efecto y varianza compartida \(R^2\)
3 / 50

Resumen

  • Reporte de correlación: además de reportar la intensidad y el sentido, acompañar reporte de tamaño de efecto y varianza compartida \(R^2\)

  • Correlación de Spearman: apropiada para variables ordinales, equivale a la correlación de Pearson del ranking de las variables

3 / 50

Resumen

  • Reporte de correlación: además de reportar la intensidad y el sentido, acompañar reporte de tamaño de efecto y varianza compartida \(R^2\)

  • Correlación de Spearman: apropiada para variables ordinales, equivale a la correlación de Pearson del ranking de las variables

  • Matriz de correlaciones: forma tradicional de reporte de asociaciones de las variables de una investigación, importante considerar tratamiento de datos perdidos (listwise o pairwise)

3 / 50

Contenidos

1- Resumen sesión anterior

2- Inferencia y muestras

3- Aleatoridad y probabilidad

4- Curva normal y puntajes Z

4 / 50

Inferencia: la otra parte del análisis

Cuando se analizan datos, 2 cosas principales

  • cálculo del estadístico:

    • promedio

    • desviación estándar

    • correlación

    • ...

  • inferencia: ¿existe este estadístico en la población?

    • probabilidad

    • error

    • significación

5 / 50

6 / 50

Motivación:

7 / 50

Inferencia

¿En qué medida se pueden relacionar resultados que se encuentran en un (sub)conjunto de unidades con lo que ocurre en general?

8 / 50

Inferencia

¿En qué medida se pueden relacionar resultados que se encuentran en un (sub)conjunto de unidades con lo que ocurre en general?

Ej: si en un subconjunto de la población encuentro que el promedio de matemáticas es mayor en mujeres que en hombres ¿es esto un reflejo de lo que ocurre en general, o se debe solo al azar? ¿se puede extrapolar a la poblacion?

8 / 50

mapa y territorio, Borges lidiando con el caos y la incertidumbre la domesticación de la casualidad error

En aquel Imperio, el Arte de la Cartografía logró tal Perfección que el mapa de una sola Provincia ocupaba toda una Ciudad, y el mapa del Imperio, toda una Provincia. Con el tiempo, estos Mapas Desmesurados no satisficieron y los Colegios de Cartógrafos levantaron un Mapa del Imperio, que tenía el tamaño del Imperio y coincidía puntualmente con él.

Menos Adictas al Estudio de la Cartografía, las Generaciones Siguientes entendieron que ese dilatado Mapa era Inútil y no sin Impiedad lo entregaron a las Inclemencias del Sol y los Inviernos. En los desiertos del Oeste perduran despedazadas Ruinas del Mapa, habitadas por Animales y por Mendigos; en todo el País no hay otra reliquia de las Disciplinas Geográficas.

Suárez Miranda, Viajes de Varones Prudentes, Libro Cuarto, Cap. XLV, Lérida, 1658.

9 / 50

En aquel Imperio, el Arte de la Cartografía logró tal Perfección que el mapa de una sola Provincia ocupaba toda una Ciudad, y el mapa del Imperio, toda una Provincia. Con el tiempo, estos Mapas Desmesurados no satisficieron y los Colegios de Cartógrafos levantaron un Mapa del Imperio, que tenía el tamaño del Imperio y coincidía puntualmente con él.

Menos Adictas al Estudio de la Cartografía, las Generaciones Siguientes entendieron que ese dilatado Mapa era Inútil y no sin Impiedad lo entregaron a las Inclemencias del Sol y los Inviernos. En los desiertos del Oeste perduran despedazadas Ruinas del Mapa, habitadas por Animales y por Mendigos; en todo el País no hay otra reliquia de las Disciplinas Geográficas.

Suárez Miranda, Viajes de Varones Prudentes, Libro Cuarto, Cap. XLV, Lérida, 1658.

Borges - Del Rigor de la Ciencia

9 / 50

Conceptos claves de inferencia

  • La inferencia en estadística se refiere a la relación que existe entre los resultados obtenidos basados en nuestra muestra y la población
10 / 50

Conceptos claves de inferencia

  • La inferencia en estadística se refiere a la relación que existe entre los resultados obtenidos basados en nuestra muestra y la población
  • ¿En qué medida podemos hacer inferencias desde nuestra muestra a la población?
10 / 50

Conceptos claves de inferencia

  • La inferencia en estadística se refiere a la relación que existe entre los resultados obtenidos basados en nuestra muestra y la población
  • ¿En qué medida podemos hacer inferencias desde nuestra muestra a la población?
  • Un concepto central es la probabilidad de ERROR
10 / 50

Parámetros y estadísticos

Población (parámetro) Muestra (estadístico)
Promedio \(\mu\) \(\bar{x}\)
Varianza \(\sigma²\) \(s²\)
Desviación estándar \(\sigma\) \(s\)
Correlación \(\rho\) \(r\)
11 / 50

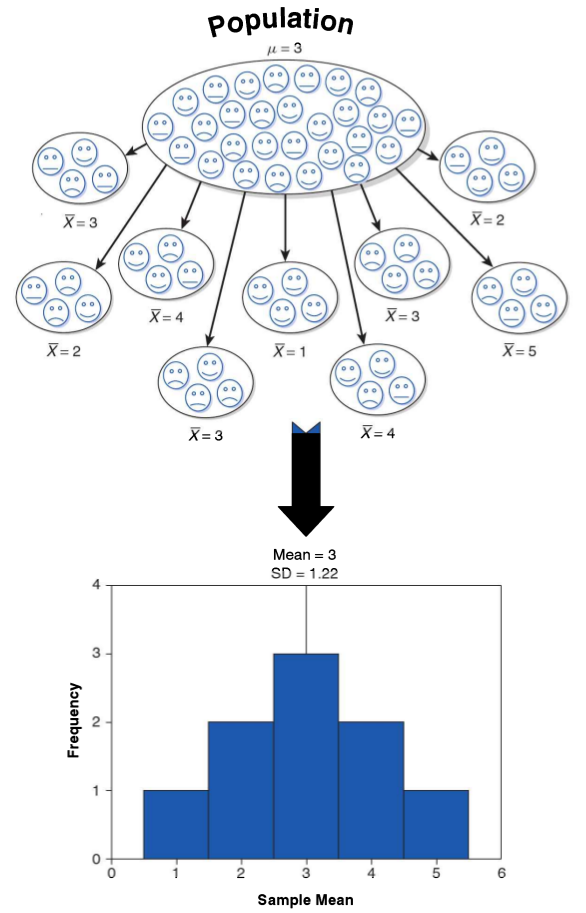
Muestreo y variabilidad

¿Cómo es posible que la media x̄ obtenida a partir de una muestra de unos pocos hogares de todos los del país, pueda ser una estimación precisa de µ?

Una segunda muestra aleatoria obtenida en el mismo momento estaría formada por hogares distintos y, sin duda, daría un valor distinto de x̄

12 / 50

Muestreo y variabilidad

Variabilidad muestral: el valor de un estadístico varía en un muestreo aleatorio repetido

¿Cuánto varía?

¿En qué rangos?

¿Qué tan probable es el rango de variación?

¿Es un rango aceptable en términos de investigación social?

13 / 50

Contenidos

1- Resumen sesión anterior

2- Inferencia y muestras

3- Aleatoridad y probabilidad

4- Curva normal y puntajes Z

14 / 50

15 / 50

Aleatoriedad y probabilidad

Llamamos a un fenómeno aleatorio si los resultados individuales son inciertos y, sin embargo, existe una distribución regular de los resultados después de un gran número de repeticiones.

16 / 50

Aleatoriedad y probabilidad

Llamamos a un fenómeno aleatorio si los resultados individuales son inciertos y, sin embargo, existe una distribución regular de los resultados después de un gran número de repeticiones.

La probabilidad de cualquier resultado de un fenómeno aleatorio es la proporción de veces que el resultado se da después de una larga serie de repeticiones

16 / 50

Azar y repetición

El comportamiento del azar es impredecible con pocas repeticiones pero presenta un comportamiento regular y predecible con muchas repeticiones.

17 / 50

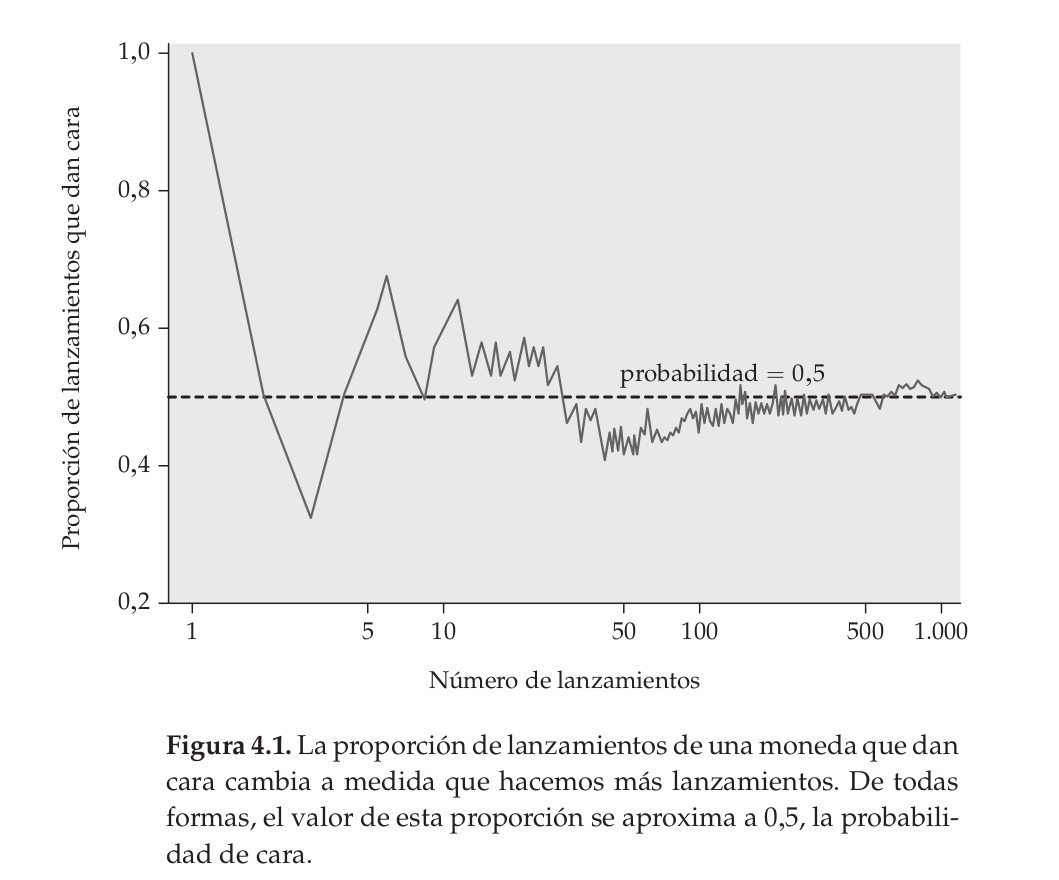
(Dato freak)

Cerca del año 1900, el estadístico inglés Karl Pearson lanzó al aire una moneda 24.000 veces. El resultado: 12.012 caras, una proporción de 0,5005.

18 / 50

Dados

Tenemos 1 dado, cuál es la probabilidad de que salga 3 al lanzarlo?

  • Espacio muestral S= conjunto de todos los resultados posibles

$$S=\{1,2,3,4,5,6\}$$

  • N del espacio muestral= 6 sucesos posibles

  • Probabilidad de que salga 3 al tirar el dado= \(\frac{1}{6}=0.166\)

19 / 50

Un modelo de probabilidad para un fenómeno aleatorio consiste en un espacio muestral S y una asignación de probabilidades P.

El espacio muestral \(S\) es el conjunto de todos los resultados posibles de un fenómeno aleatorio.

Un suceso es un conjunto de resultados. P asigna un número P(A) a un suceso A como su probabilidad.

20 / 50

Reglas modelo de probabilidad

21 / 50

Dados, probabilidades y distribuciones

Ejercicio:

  • probar lanzando 1 dado repetidas veces

  • probar con 2 dados

  • ... y con 6

-> link

22 / 50

Dados, probabilidades y áreas

23 / 50

Dados, probabilidades y áreas

24 / 50

Dados, probabilidades y áreas

25 / 50

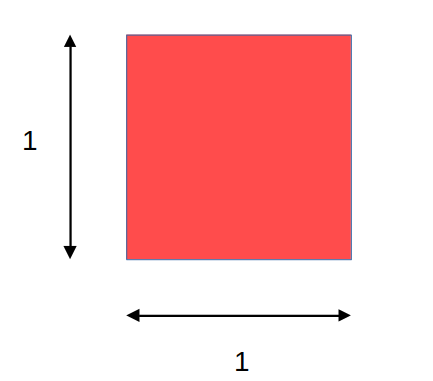
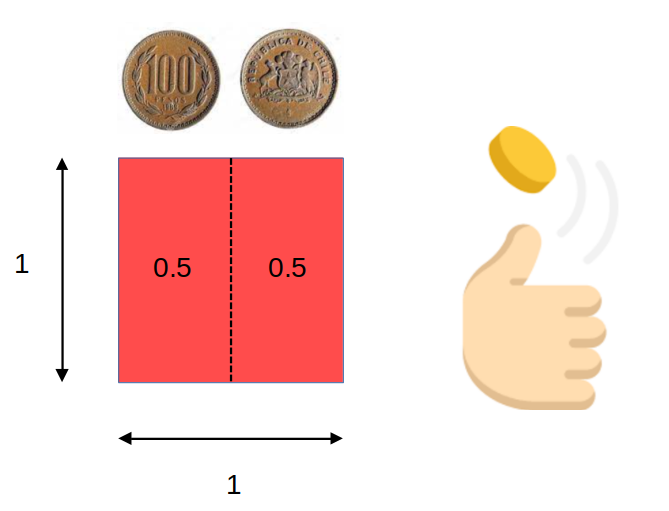
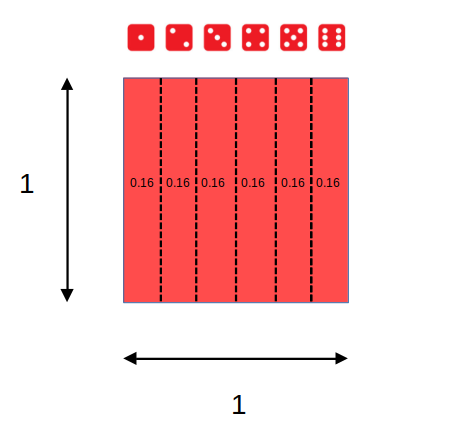
Dados, probabilidades y áreas


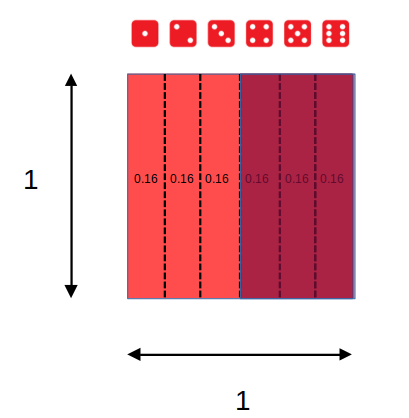
Eventos posibles (espacio muestral S) = 6 = (1,2,3,4,5,6)

\begin{align*} P(x)\geq4&=P(4)+P(5)+P(6) \\ &=0.1\overline{6}+0.1\overline{6}+0.1\overline{6} \\ &=0.5 \end{align*}

26 / 50

Sucesos con distinta probabilidad

Ej: suma de 3 dados al azar repetidos

27 / 50

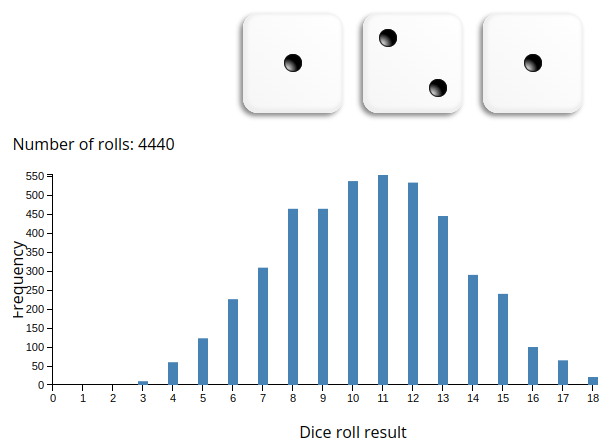
Histograma

Frecuencias o probabilidad de cada evento

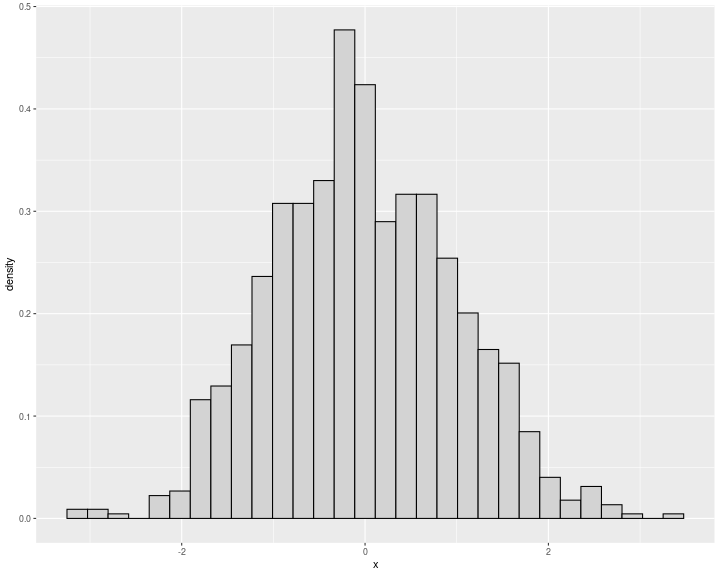
Curvas de densidad

Modelo matemático de la distribución

28 / 50

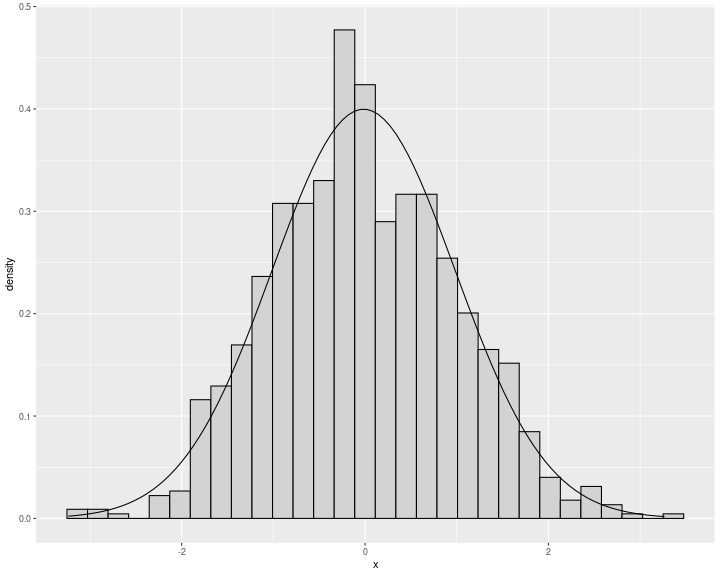
Curva de densidad

  • describe el aspecto general de una distribución

  • se halla siempre en el eje de las abscisas o por encima de él, y define por debajo un área exactamente igual a 1.

  • El área por debajo de la curva, y entre cualquier intervalo de valores, es la proporción de todas las observaciones que están situadas en dicho intervalo.

29 / 50

Contenidos

1- Resumen sesión anterior

2- Inferencia y muestras

3- Aleatoridad y probabilidad

4- Curva normal y puntajes Z

30 / 50

Distribuciones normales

  • clase particular de curvas de densidad

  • simétricas y con un solo punto de elevación

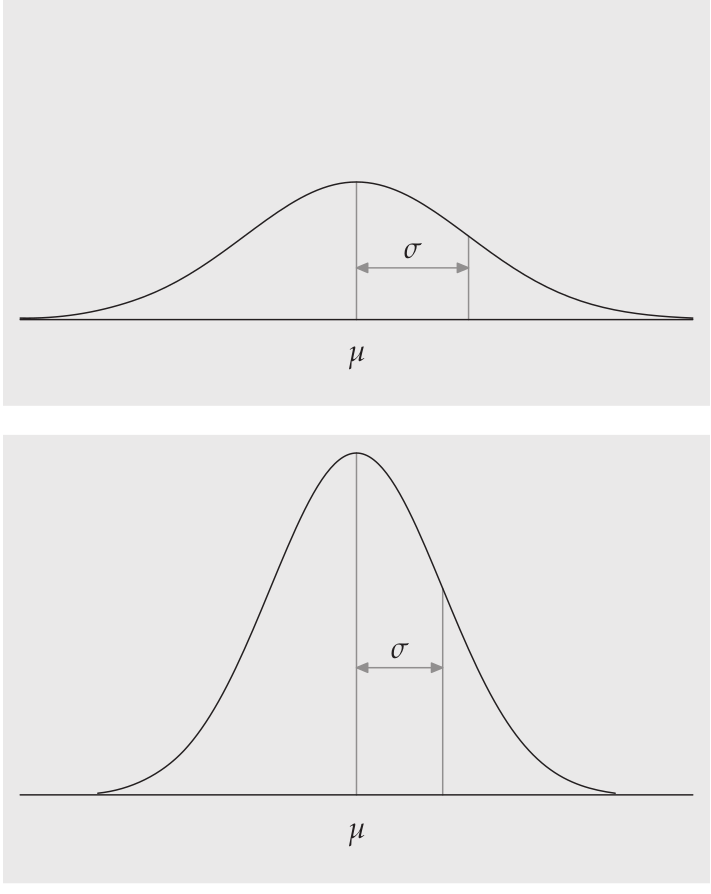
  • la media se sitúa al centro, y la desviación estandar expresa su dispersión

  • la pendiente es más fuerte cerca del centro, y se suaviza hacia los extremos

  • Los puntos en los que tiene lugar este cambio de curvatura se hallan a una distancia σ, a ambos lados de la media µ.

31 / 50

32 / 50

¿Por qué son importantes las distribuciones normales en estadística?

  • las distribuciones normales son buenas descripciones de algunas distribuciones de datos reales

  • buenas aproximaciones a los resultados de muchos tipos de fenómenos aleatorios (ej: lanzar dados)

  • permiten realizar inferencia estadística sobre fenómenos basados en distribuciones normales

33 / 50

Relación entre áreas bajo la curva normal y probabilidades

34 / 50

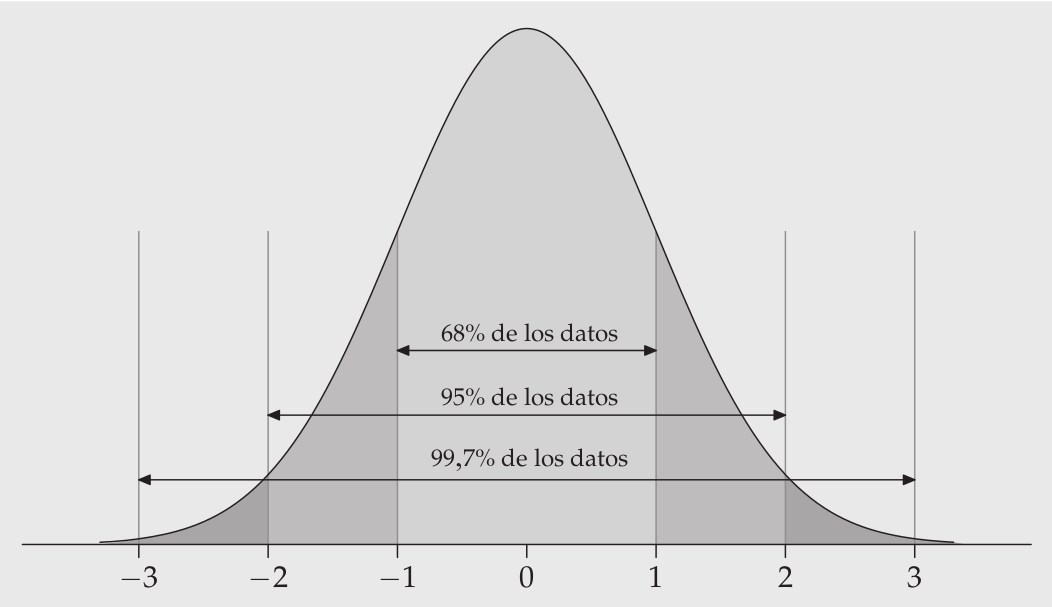
Regla del 68-95-99,7

En una distribución normal de media \(\mu\) y desviación estándar \(\sigma\):

  • El 68% de todas las observaciones se encuentran dentro del intervalo µ ± σ.

  • El 95% de todas las observaciones se encuentran dentro del intervalo µ ± 2σ.

  • El 99,7% de todas las observaciones se encuentran dentro del in- tervalo µ ± 3σ.

35 / 50

36 / 50

Ejemplo:

Estatura promedio mujeres en Chile: 160 cm Desviación estándar: 5 cm

¿Qué podemos decir basándonos en la distribución normal?

37 / 50

Ejemplo:

Estatura promedio mujeres en Chile: 160 cm Desviación estándar: 5 cm

¿Qué podemos decir basándonos en la distribución normal?

  • el 68% de las mujeres se encuentra entre 155 y 165cm

  • el 95% de las mujeres se encuentra entre 150 y 170cm

  • solo un 5% de las mujeres mide más de 170cm

  • prácticamente todas las mujeres (99.7) se encuentran entre 145 y 175cm
37 / 50

Valores \(z\) y estandarización

  • estandarización: expresar el valor de una distribución en términos de desviaciones estándar basados en la distribución normal

  • para estandarizar un valor, se le resta la media y se divide por la desviación estándar

$$z=\frac{x-\mu}{\sigma}$$

  • los valores estandarizados se denominan valores z
38 / 50

Valores \(z\) y estandarización

  • Un valor z nos dice a cuántas desviaciones típicas se encuentra la observación original de la media y en qué dirección.

  • Las observaciones mayores que la media son positivas y las menores, negativas.

39 / 50

Siguiendo con el ejemplo anterior de estatura de mujeres \(\bar{x}=160\) y \(\sigma=5\), la estatura estandarizada es:

$$z=\frac{altura-160}{5} $$

Por ejemplo, una mujer que mide 165:

$$z=\frac{165-160}{5}=\frac{5}{5}=1$$

Su puntaje \(z\) nos dice que está una desviación estandar sobre el promedio

40 / 50

Puntajes \(z\) y proporciones

Los valores \(z\) permiten calcular la proporción de casos bajo la curva normal que están sobre y bajo el puntaje

Por ejemplo, para el caso de 1 desviación sobre el promedio, el área bajo la curva bajo este puntaje sería:

41 / 50






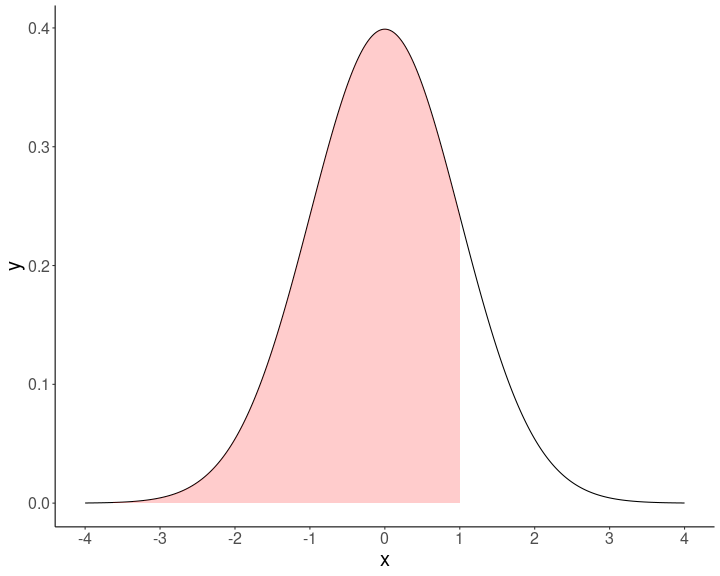
En base a la distribución normal sabemos que bajo 1 desviación estańdar está el 68% de los datos + la cola izquierda de la curva, que es (100-68/2)=16%.

Por lo tanto 84% (68+16) de los casos tienen una estatura menor a 165 cm

42 / 50
  • Ej: estatura de 152cm

\begin{align*} z&=\frac{x-\mu}{\sigma}\\\\ z&=\frac{altura-160}{5}\\\\ z&=\frac{152-160}{5}=\frac{-8}{5}=-1.6 \end{align*}

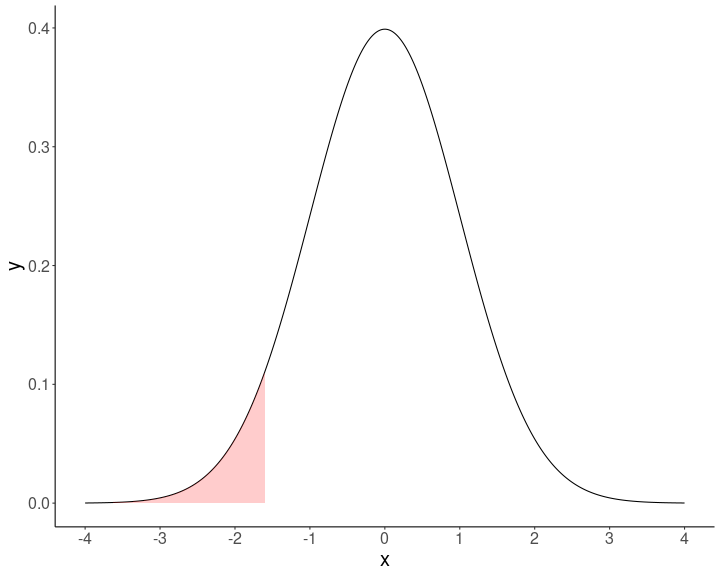
¿Cómo calcular el área bajo la curva para un valor específico?

43 / 50

Tabla de Puntajes Z

44 / 50

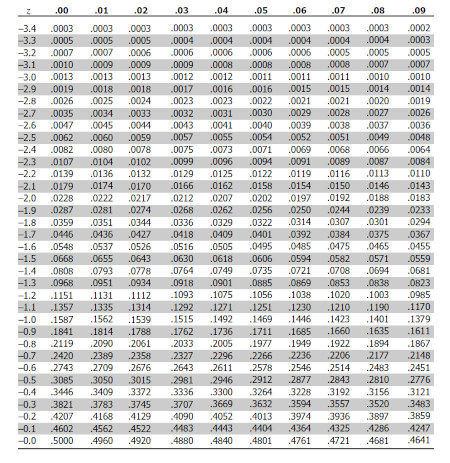
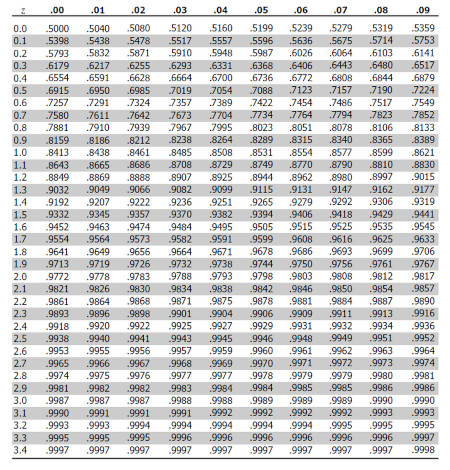
Tabla de Puntajes Z

  • El valor correspondiente a -1.6 en la tabla de valores Z se busca en la fila Z -1.6 y la columna 0.00 (ya que la centésima de -1.6 es 0).

  • = 0.0548, es decir, alrededor de un 5% de los casos se enceuntra bajo esa estatura (152 cm)

  • en R= 
pnorm(q=-1.6)
[1] 0.05479929
45 / 50

Resumen

  • inferencia: ¿con qué probabilidad podemos decir que lo que calculamos en nuestra muestra existe en la población?

  • probabilidades y distribución normal

  • puntajes Z y área bajo la curva normal

46 / 50

Próxima semana: Distribuciones muestrales, error estándar e intervalos de confianza

  • ¿Qué tan probable es que un resultado obtenido en una muestra se deba al azar?

  • ¿Cómo nos sirve la curva normal para contrastar hipótesis de investigación?

  • ¿Con qué nivel de confianza podemos afirmar que nuestra hipótesis es verdadera?

47 / 50

Lectura:

Moore cap. 6 - Introducción a la inferencia estadística

48 / 50

ASISTENCIA






bit.ly/correlacional-asistencia

49 / 50

Estadística Correlacional

Asociación, inferencia y reporte

Juan Carlos Castillo

Sociología FACSO - UChile

2do Sem 2023

correlacional.netlify.com

50 / 50

Contenidos

1- Resumen sesión anterior

2- Inferencia y muestras

3- Aleatoridad y probabilidad

4- Curva normal y puntajes Z

2 / 50
Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
oTile View: Overview of Slides
sToggle scribble toolbox
Esc Back to slideshow