class: front .pull-left-wide[ # Estadística Correlacional] .pull-right-narrow[] ## Asociación, inferencia y reporte ---- .pull-left[ ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 2do Sem 2023 ## [.orange[correlacional.netlify.com]](https:/correlacional.netlify.com) ] .pull-right-narrow[ .center[ .content-block-gray[ ## Sesión 6: ## .orange[Inferencia 2: Error e intervalos de confianza]] ] ] --- layout: true class: animated, fadeIn --- class: roja right .pull-left-narrow[ # .black[Contenidos] ] .pull-right-wide[ ## .yellow[1- Resumen sesión anterior] ## 2- Distribución muestral del promedio ## 3- Error estándar ## 4- Intervalos de confianza ] --- # Inferencia: la otra parte del análisis Cuando se analizan datos, 2 cosas principales .pull-left[ .content-box-yellow[ - cálculo del estadístico: - promedio - desviación estándar - correlación - ... ] ] .pull-right[ .content-box-red[ - inferencia: ¿existe este estadístico en la población? - probabilidad - error - significación ] ] --- # Parámetros y estadísticos ---- | | Población (parámetro) | Muestra (estadístico) | |--------------------- |------------ |--------- | | Promedio | `\(\mu\)` | `\(\bar{x}\)` | | Varianza | `\(\sigma²\)` | `\(s²\)` | | Desviación estándar | `\(\sigma\)` | `\(s\)` | | Correlación | `\(\rho\)` | `\(r\)` | --- # Muestreo y variabilidad ¿Cómo es posible que la media x̄ obtenida a partir de una muestra de unos pocos hogares de todos los del país, pueda ser una estimación precisa de µ? -- Una segunda muestra aleatoria obtenida en el mismo momento estaría formada por hogares distintos y, sin duda, daría un valor distinto de x̄ -- Por lo tanto: ¿cómo podemos .red[confiar] en los estadísticos de una muestra? --- # Muestreo y variabilidad **Variabilidad muestral**: el valor de un estadístico varía en un muestreo aleatorio repetido ¿Cuánto varía? ¿En qué rangos? ¿Qué tan **probable** es el rango de variación? ¿Es un rango aceptable en términos de investigación social? --- # Dados, probabilidades y áreas .pull-left[ 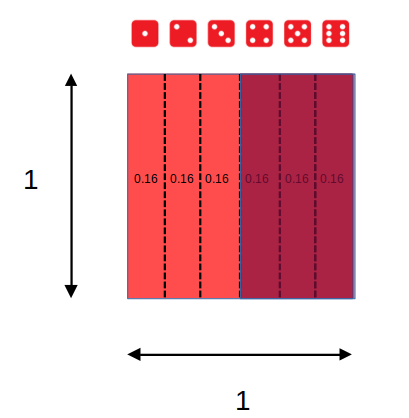 ] .pull-right[ <br> Eventos posibles (espacio muestral S) = 6 = (1,2,3,4,5,6) `\begin{align*} P(x)\geq4&=P(4)+P(5)+P(6) \\ &=0.1\overline{6}+0.1\overline{6}+0.1\overline{6} \\ &=0.5 \end{align*}` ] --- # Sucesos con distinta probabilidad Ej: suma de 3 dados al azar repetidos .center[ 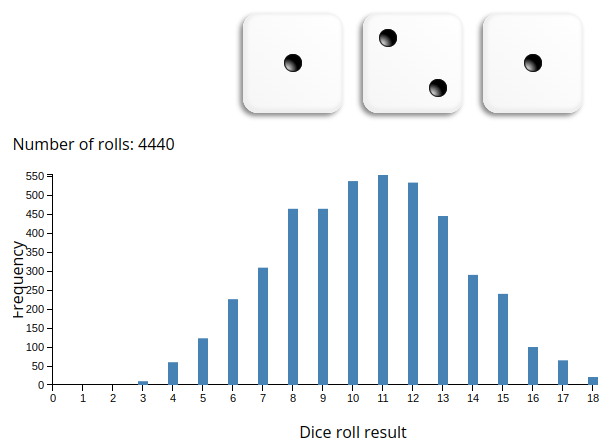 ] --- .pull-left[ ## Histograma Frecuencias o probabilidad de cada evento <!-- --> ] .pull-right[ ## Curvas de densidad Modelo matemático de la distribución <!-- --> ] --- # ¿Por qué son importantes las distribuciones normales en estadística? - las distribuciones normales son buenas descripciones de algunas distribuciones de datos reales - permiten realizar **inferencia estadística** sobre la probabilidad de ocurrencia de ciertos fenómenos basados en distribuciones normales --- ## Distribución normal estándar 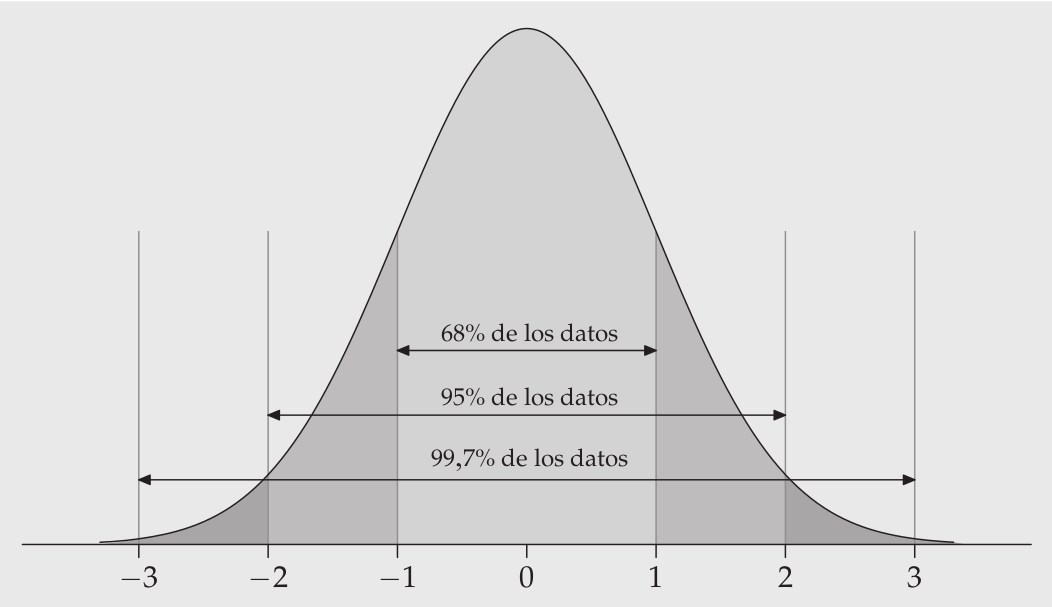 --- # Valores `\(z\)` y estandarización - estandarización: expresar el valor de una distribución en términos de desviaciones estándar basados en la distribución normal - para estandarizar un valor, se le resta la media y se divide por la desviación estándar `$$z=\frac{x-\mu}{\sigma}$$` - los valores estandarizados se denominan .red[valores z] --- # Puntajes `\(z\)` y proporciones .pull-left[ Los valores `\(z\)` permiten calcular la proporción de casos bajo la curva normal que están sobre y bajo el puntaje Por ejemplo, para el caso de 1 desviación sobre el promedio, el área bajo la curva bajo este puntaje sería: ] .pull-right[ <!-- --> ] --- class: middle .pull-left[ ## Curva normal, puntajes Z y proporciones  ] .pull-right[ .medium[ <br> <br> <br> Siguiendo con el ejemplo de altura `\(\bar{x}=160,\sigma=5\)` `$$z=\frac{x-\mu}{\sigma}=\frac{165-160}{5}=1$$` En base a la distribución normal sabemos que bajo 1 desviación estańdar está el 68% de los datos + la cola izquierda de la curva, que es (100-68/2)=16%. Ej: 84% (68+16) de los casos tienen una estatura menor a 165 cm ]] --- class: roja right .pull-left-narrow[ # .black[Contenidos] ] .pull-right-wide[ ## 1- Resumen sesión anterior ## .yellow[2- Distribución muestral del promedio] ## 3- Error estándar ## 4- Intervalos de confianza ] --- # Inferencia ¿En qué medida se pueden relacionar resultados que se encuentran en una .green[muestra] (subconjunto de unidades) con lo que ocurre .red[en general]? -- .medium[ - Ej: si en un subconjunto de la población encuentro que el promedio de matemáticas es mayor en mujeres que en hombres ¿se puede .green[extrapolar] a la población, o se debe solo al .red[azar]? ] -- .content-box-red[ .center[ -> .red[¿Bajo qué normas o reglas estoy dispuest_ a .green[confiar] en que lo que obtuve con mi muestra (ej: un promedio) ocurre efectivamente en la población?]]] ??? ¿le creo o no le creo al promedio de una muestra? ¿qué tendría que pasar para que le creyera? mapa y territorio, Borges lidiando con el caos y la incertidumbre la domesticación de la casualidad error --- class: inverse ### Principios de la ciencia (Merton) - **Universalismo**: cualquier persona puede contribuir al conocimiento científico, independiente de su origen. - **Desinterés**: la conducta de investigadores debe estar orientada por la búsqueda de la verdad, no con intereses personales ni monetarios. - **Comunalidad**: los hallazgos de la ciencia pertenecen a la comunidad y no a quién los descubrió. - .red[**Escepticismo organizado**: los hallazgos no se aceptan porque sí, se requieren pruebas.] --- class: roja # ¿Qué .yellow[pruebas] se requieren para que se pueda .orange[confiar] en que un resultado obtenido con una muestra ocurra en la población? --- # Ejercicio - tenemos una población de (ej.) 200 - en esta población existen 6 niveles educacionales, homogéneamente distribuidos (cada nivel educacional equivale a a 1/6 de la población) - por lo tanto, el nivel educacional promedio de la población equivale a 1+2+3+4+5+6/6= 3.5 --- # Ejercicio: Muestra aleatoria y error - cada persona selecciona al azar a 5 sujetos (5 dados) y les "pregunta" su nivel educacional (cara superior del dado luego de tirarlo) - sacar el promedio de cada muestra - ¿qué tanto varían los promedios? -> registro [aquí](https://docs.google.com/spreadsheets/d/1YrMd_ds5zHgQWrdjYcX5Diwv7bQHDzf5r2A0oYWriyA/edit#gid=0) ??? --- # Distribución muestral del promedio .pull-left-narrow[  ] .pull-right-wide[ - Si tengo la desviación estándar de los promedios, puedo construir un .red[intervalo] de probabilidad, basado en la curva normal - En lenguaje de inferencia no digo que mi promedio es=10, sino un rango (intervalo) y un cierto nivel de probabilidad ] --- class: roja ## .yellow[Problema: tenemos 1 SOLA MUESTRA, y un solo promedio] # ¿Cómo obtenemos entonces la desviación estándar del promedio? --- class: roja right .pull-left-narrow[ # .black[Contenidos] ] .pull-right-wide[ ## 1- Resumen sesión anterior ## 2- Distribución muestral del promedio ## .yellow[3- Error estándar] ## 4- Intervalos de confianza ] --- .pull-left-narrow[  ] .pull-right-wide[ .content-box-purple[ ## Desviación estándar y error estándar] - más que el promedio de la variable en nuestra **muestra**, en inferencia nos interesa estimar en qué medida ese promedio da cuenta del promedio de la **población** {{content}} ] -- - contamos con **una muestra**, pero sabemos que otras muestras podrían haber sido extraídas, probablemente con distintos resultados. --- # Distribución muestral del promedio  --- # Distribución muestral del promedio  --- # Distribución muestral del promedio  --- # Teorema del límite central - la distribución de los promedios de distintas muestras - o .red[distribución muestral del promedio] - se aproxima a una distribución normal -- - En muestras mayores a 30 la desviación estándar de los promedios (error estándar del promedio) equivale a: `$$\sigma_{\bar{X}}=SE(error estándar)=\frac{s}{\sqrt{N}}$$` - `\(s\)` = desviación estándar de la muestra - `\(N\)` = tamaño de la muestra --- class: inverse ## Basados en el .red[teorema del límite central], es posible calcular la desviación estándar del promedio (error estándar) con .red[una sola muestra] -> ver demostración [aquí](https://docs.google.com/spreadsheets/d/1YrMd_ds5zHgQWrdjYcX5Diwv7bQHDzf5r2A0oYWriyA/edit#gid=0) --- class: inverse middle right # ¿Para qué nos sirve el .red[error estándar] o .red[SE] del promedio? ##(... y de otros estadísticos, como la correlación) --- # Usos del error estándar - Dos usos complementarios: - construcción de intevalos de confianza - test de hipótesis (próxima clase) --- class: roja right .pull-left-narrow[ # .black[Contenidos] ] .pull-right-wide[ ## 1- Resumen sesión anterior ## 2- Distribución muestral del promedio ## 3- Error estándar ## .yellow[4- Intervalos de confianza] ] --- # Intervalos y probabilidad .pull-left-narrow[ .medium[ - Nuestro promedio muestral `\(\bar{x}\)` posee una distribución normal con una desviación estandar = SE (error estándar) - Esto nos permite estimar probabilidades basados en los valores de la curva normal ] ] .pull-right-wide[ .center[]] --- # Intervalos de confianza .pull-left-wide[ .center[]] .pull-right-narrow[ .medium[ - Por ejemplo, un intervalo de confianza de `\(\bar{x}\pm1.96SE\)` abarca aproximadamente el 95% de los valores probables - En este caso, puedo decir que el promedio se encuentra en un rango de valores con un .red[nivel de confianza] de 95% ] ] --- ## Ejemplo: intervalo de confianza para un promedio ---- .pull-left[ .content-box-green[ - Tenemos: - promedio de ingresos: 800.000 - desviación estándar: 100.000 - N muestral: 1.600 ]] .pull-right[ `\begin{align*} SE&=\frac{s}{\sqrt{N}} \\\\ &=\frac{100.000}{\sqrt{1.600}} \\\\ &=\frac{100.000}{40}=2.500 \end{align*}` ] --- - Tenemos: `\(SE=2.500\)`, `\(\bar{x}_{ingresos}=800.000\)` - Con estos valores podemos construir un rango de probabilidad basado en la curva normal, sumando y restando errores estándar - Por ejemplo, `\(\bar{x}{\color{red}\pm}1.96SE\)` abarcan el 95% de los valores alrededor del promedio - `\(800.000 - (1.96*2.500) = 800.000 - 4.900={\color{red}{795.100}}\)` - `\(800.000 + (1.96*2.500) = 800.000 + 4.900={\color{red}{804.900}}\)` - Por lo tanto, podemos decir .red[con un 95% de confianza] que el promedio de ingresos se encuentra entre 795.100 y 804.900 --- # ¿Confianza en qué? - bajo esta lógica, la confianza está en que si tuvieramos la posibilidad de extraer múltiples muestras, el 95% de las veces nuestro intervalo contendría el promedio - o que existe un 5% de probabilidad de error, es decir, que el promedio de la muestra no sea el de la población - o que las chances de error son 1 de 20 --- class: roja # Un .yellow[intervalo de confianza] (IC o CI) es la mejor estimación del rango de un estadístico en la población (parámetro poblacional) con una muestra aleatoria --- .center[  ] --- class: inverse middle ## ¿De qué depende el .red[tamaño] del intervalo de confianza? ## ¿Cómo se establece el .red[nivel de confianza] del intervalo? --- ## ¿De qué depende el tamaño del intervalo de confianza? - recordemos que el intervalo de confianza se elabora sumando y restando errores estándar al promedio `$$\sigma_{\bar{X}}=SE(error estándar)=\frac{s}{\sqrt{N}}$$` -- - dado que el tamaño muestral (N) se encuentra en el denominador del `\(SE\)`, a mayor N, menor será el `\(SE\)` y menor el intervalo de confianza - esto tiene implicancias directas en el cálculo del tamaño muestral --- # ¿De qué depende el nivel de confianza? - en estadística inferencial, la confianza se asocia a un nivel de probabilidad de error - la probabilidad de error a aceptar no es un criterio estadístico, es convencional - por convención, se acepta como estadísticamente significativa una probabilidad de error menor al 5%, asociada a un intervalo de confianza de `\(\pm1.96SE\)` (usando la distribución `\(Z\)`) --- class: inverse # Resumen - distribución muestral del promedio - error estándar - intervalos de confianza --- # Lectura: [Moore cap. 7 - Inferencia para medias y desviaciones típicas](https://correlacional.netlify.app/files/textos/Moore.pdf) # Recomendaciones Ver [simulación de intervalo de confianza para promedio muestral](https://shiny.rit.albany.edu/stat/confidence/) --- # ASISTENCIA .pull-left[  ] .pull-right[ <br> <br> <br> <br> <br> bit.ly/correlacional-asistencia ] --- class: front .pull-left-wide[ # Estadística Correlacional] .pull-right-narrow[] ## Asociación, inferencia y reporte ---- .pull-left[ ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 2do Sem 2023 ## [.orange[correlacional.netlify.com]](https://encuestas-sociales.netlify.com) ]