class: front .pull-left-wide[ # Estadística Correlacional] .pull-right-narrow[] ## Asociación, inferencia y reporte ---- .pull-left[ ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 2do Sem 2023 ## [.orange[correlacional.netlify.com]](https:/correlacional.netlify.com) ] .pull-right-narrow[ .center[ .content-block-gray[ ## Sesión 8: ## .orange[Inferencia 4: Hipótesis direccionales y proporciones]] ] ] --- layout: true class: animated, fadeIn --- # Lectura hoy: [Moore cap. 8 - Inferencia para proporciones](https://correlacional.netlify.app/files/textos/Moore.pdf) --- # Resumen clase anterior - **hipótesis**: aseveraciones sobre algo que ocurre en la población, usualmente asociaciones entre conceptos / variables - el contraste de hipótesis en estadística opera mediante el rechazo de la **hipótesis nula** (o de no diferencias), con una probabilidad de error `\(\alpha\)` - para diferencia de medias se utiliza la prueba t, que básicamente es una distribución normal ajustada al tamaño muestral --- ## Tipos de preguntas e hipótesis (ej: con promedio(s)) ---- .small[ | **Pregunta**| **Hipotesis** | **Prueba** |---------------------|------------------------------------------------------| | A. ¿Existe el promedio en la población? <br> | `$$H_{a}: \bar{X}_1 \neq 0$$` `$$H_{0}: \bar{X}_1 = 0$$` | Dos colas (no direccional) | B. ¿Existen diferencias de promedios en la población? | `$$H_{a}: \bar{X}_1 - \bar{X}_2 \neq 0$$` `$$H_{0}: \bar{X}_1 - \bar{X}_2= 0$$` | Dos colas (no direccional) | C. ¿Es un promedio (1) superior (o inferior) al otro (2)? | `$$H_{a}: \bar{X}_1 - \bar{X}_2 \gt 0$$` `$$H_{0}: \bar{X}_1 - \bar{X}_2 \leq 0$$` | Una cola (direccional) - ] --- class: center middle  --- class: middle center  --- .content-box-red[ # BUSCAMOS RECHAZAR LA HIPÓTESIS NULA] - Recordar que nuestra hipótesis de investigación es la .red[hipótesis alternativa] - La .blue[hipótesis nula] (cero) expresa que lo que nosotros buscamos no existe o ES CERO en la población - Si logramos rechazar `\(H_0\)` entonces hay sustento para nuestra hipótesis de investigación --- # Los cinco pasos de la inferencia 1. Establecer las hipótesis (y definir si son o no direccionales) 2. Calcular error estándar 3. Estimar estadístico de prueba (ej: Z o t) 4. Establecer valor crítico de la prueba (de acuerdo a un cierto nivel de confianza) 5. Contraste e interpretación ->posibilidad de calcular intervalo de confianza --- # Sobre los cinco pasos de la inferencia - Definir estos pasos y realizar los cálculos paso a paso tiene un sentido procedimiental y pedagógico - Mediante el uso de software (como R) es suficiente con paso 1 (hipótesis) y paso 5 (interpretación) - Pero ... para hacer una buena interpretación, es importante saber qué ocurre tras bambalinas en el contraste de hipótesis --- class: roja right .pull-left-narrow[ .left[ ### .black[Contenidos] ] ] .pull-right-wide[ ## .yellow[1- Repaso hipótesis de diferencia de medias] ## 2- Hipótesis direccionales ## 3- Hipótesis para proporciones ## 4- Inferencia en correlación ] --- # Datos Vamos a generar una submuestra de 350 casos de CASEN para ilustrar de mejor manera el sentido del test de hipótesis ```r pacman::p_load(sjmisc, haven, dplyr, stargazer, interpretCI, kableExtra) load("casen2022_inf2.Rdata") options(scipen=999) # para evitar notación en los ceros set.seed(20) # para fijar el resultado aleatorio casen_350 <- casen2022_inf %>% select(salario,sexo) %>% sample_n(350) casen_350 <- na.omit(casen_350) ``` --- # Datos ```r stargazer(as.data.frame(casen_350), type = "text") ``` ``` ====================================================== Statistic N Mean St. Dev. Min Max ------------------------------------------------------ salario 343 634,402.300 459,180.200 30,000 2,900,000 sexo 343 1.402 0.491 1 2 ------------------------------------------------------ ``` --- ```r casen_350%>% # se especifica la base de datos dplyr::group_by(sexo=sjlabelled::as_label(sexo)) %>% # se agrupan por la variable categórica y se usan sus etiquetas con as_label dplyr::summarise(Obs.=n(),Promedio=mean(salario, na.rm=TRUE),SD=sd(salario, na.rm=TRUE)) %>% # se agregan las operaciones a presentar en la tabla kable(, format = "markdown") # se genera la tabla ``` |sexo | Obs.| Promedio| SD| |:---------|----:|--------:|--------:| |1. Hombre | 205| 654585.4| 468692.5| |2. Mujer | 138| 604420.3| 444666.0| --- ## Hipótesis de diferencia de medias ### Paso 1: Establecimiento de hipótesis El salario promedio de las mujeres es distinto al de los hombres `$$H_{a}: \bar{X}_1 - \bar{X}_2 \neq 0$$` `$$H_{0}: \bar{X}_1 - \bar{X}_2= 0$$` --- ## Hipótesis de diferencia de medias ### Paso 2: Cálculo del error estándar (para diferencia de medias) `$$SE=\sqrt{\frac{\sigma_{diff}}{n_a}+\frac{\sigma_{diff}}{n_b}}$$` Donde `$$\sigma_{diff}=\frac{\sigma^2_{a}(n_a-1)+\sigma^2_{b}(n_b-1)}{n_a+n_b-2}$$` --- Cálculo de la desviación estándar de las diferencias de promedios: `\begin{align*} \sigma_{diff}&=\frac{468692^2(205-1)+444666^2(138-1)}{205+138-2} \\ \\ &=\frac{44813126936256+27088715663172}{341}\\ \\ &=210855843400 \end{align*}` --- Y enfonces el error estándar de la diferencia de medias: `\begin{align*} SE&=\sqrt{\frac{\sigma_{diff}}{n_a}+\frac{\sigma_{diff}}{n_b}} \\ \\ &=\sqrt{\frac{210855843400}{205}+\frac{210855843400}{138}}\\ \\ &=50561 \end{align*}` --- ## Hipótesis de diferencia de medias ### Paso 3: Cálculo del estadístico de prueba (t para diferencia de medias) `\begin{align*} t&=\frac{(\bar{x}_1-\bar{x}_2)}{SE_{\bar{x_1}-\bar{x_2}}} \\ \\ &=\frac{654585.4- 604420.3}{50561} \\ \\ &=\frac{50165.1}{50561} = 0.992 \end{align*}` --- ## Hipótesis de diferencia de medias ### Paso 4: Establecimiento del valor crítico de la prueba (t) .pull-left[ - para un nivel de error `\(\alpha=0.05\)` - y una hipótesis de diferencia de dos colas: `\(\alpha/2=[0.025-0.975]\)` - grados de libertad N-2= 343-2 = 341] .pull-right[ ```r qt(p=.05/2, df=341, lower.tail=FALSE) ``` ``` [1] 1.966945 ``` ] --- class: middle center 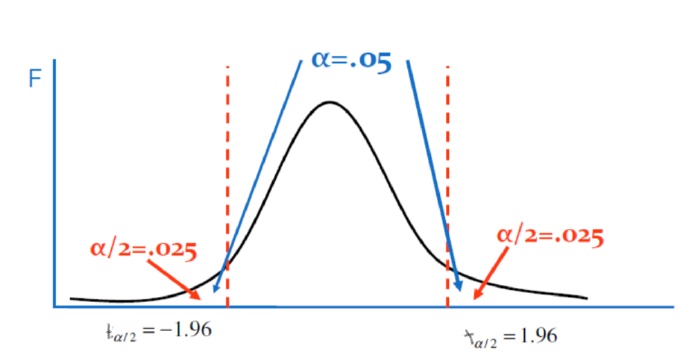 --- ## Hipótesis de diferencia de medias ### Paso 5: Contraste de hipótesis En este contraste se compara el valor estimado del estadístico de prueba y su valor crítico para dos colas: `$$t_{cri}= -1.96 < t_{est}=0.992 < t_{cri}= 1.96$$` Por lo tanto, nuestro valor estimado queda fuera de la zona de rechazo de la hipótesis nula. En consecuencia, con un nivel de confianza de 95% no podemos afirmar que existen diferencias salariales entre hombres y mujeres --- .pull-left-wide[ <!-- --> ] .pull-right-narrow[ .medium[ <br> <br> <br> <br> <br> <br> <br> El gráfico muestra nuestro valor estimado de t fuera de la zona de rechazo. Por lo tanto, no podemos rechazar `\(H_0\)`, las diferencias no son distintas de cero ] ] --- # Test de hipótesis de diferencias en R ```r t.test(salario ~ sexo, data = casen_350, var.equal=TRUE) ``` ``` Two Sample t-test data: salario by sexo t = 0.99215, df = 341, p-value = 0.3218 alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0 95 percent confidence interval: -49287.48 149617.63 sample estimates: mean in group 1 mean in group 2 654585.4 604420.3 ``` --- # tabla t test con `rempsyc` ```r pacman::p_load(rempsyc,broom) model <- t.test(salario ~ sexo, data = casen_350, var.equal=TRUE) stats.table <- tidy(model, conf.int = TRUE) nice_table(stats.table, broom = "t.test") ``` <div class="tabwid"><style>.cl-e3c10ad0{table-layout:auto;}.cl-e3ba03f2{font-family:'Times New Roman';font-size:12pt;font-weight:normal;font-style:normal;text-decoration:none;color:rgba(0, 0, 0, 1.00);background-color:transparent;}.cl-e3ba041a{font-family:'Times New Roman';font-size:12pt;font-weight:normal;font-style:italic;text-decoration:none;color:rgba(0, 0, 0, 1.00);background-color:transparent;}.cl-e3ba042e{font-family:'Times New Roman';font-size:7.2pt;font-weight:normal;font-style:normal;text-decoration:none;color:rgba(0, 0, 0, 1.00);background-color:transparent;position: relative;top:3.6pt;}.cl-e3bd3dec{margin:0;text-align:center;border-bottom: 0 solid rgba(0, 0, 0, 1.00);border-top: 0 solid rgba(0, 0, 0, 1.00);border-left: 0 solid rgba(0, 0, 0, 1.00);border-right: 0 solid rgba(0, 0, 0, 1.00);padding-bottom:5pt;padding-top:5pt;padding-left:5pt;padding-right:5pt;line-height: 2;background-color:transparent;}.cl-e3bd3e0a{margin:0;text-align:left;border-bottom: 0 solid rgba(0, 0, 0, 1.00);border-top: 0 solid rgba(0, 0, 0, 1.00);border-left: 0 solid rgba(0, 0, 0, 1.00);border-right: 0 solid rgba(0, 0, 0, 1.00);padding-bottom:5pt;padding-top:5pt;padding-left:5pt;padding-right:5pt;line-height: 2;background-color:transparent;}.cl-e3bd51e2{background-color:transparent;vertical-align: middle;border-bottom: 0.5pt solid rgba(0, 0, 0, 1.00);border-top: 0.5pt solid rgba(0, 0, 0, 1.00);border-left: 0 solid rgba(0, 0, 0, 1.00);border-right: 0 solid rgba(0, 0, 0, 1.00);margin-bottom:0;margin-top:0;margin-left:0;margin-right:0;}.cl-e3bd51f6{background-color:transparent;vertical-align: middle;border-bottom: 0.5pt solid rgba(0, 0, 0, 1.00);border-top: 0 solid rgba(0, 0, 0, 1.00);border-left: 0 solid rgba(0, 0, 0, 1.00);border-right: 0 solid rgba(0, 0, 0, 1.00);margin-bottom:0;margin-top:0;margin-left:0;margin-right:0;}.cl-e3bd520a{background-color:transparent;vertical-align: middle;border-bottom: 0.5pt solid rgba(0, 0, 0, 1.00);border-top: 0 solid rgba(0, 0, 0, 1.00);border-left: 0 solid rgba(0, 0, 0, 1.00);border-right: 0 solid rgba(0, 0, 0, 1.00);margin-bottom:0;margin-top:0;margin-left:0;margin-right:0;}</style><table data-quarto-disable-processing='true' class='cl-e3c10ad0'><thead><tr style="overflow-wrap:break-word;"><th class="cl-e3bd51e2"><p class="cl-e3bd3dec"><span class="cl-e3ba03f2">Method</span></p></th><th class="cl-e3bd51e2"><p class="cl-e3bd3dec"><span class="cl-e3ba03f2">Alternative</span></p></th><th class="cl-e3bd51e2"><p class="cl-e3bd3dec"><span class="cl-e3ba03f2">Mean 1</span></p></th><th class="cl-e3bd51e2"><p class="cl-e3bd3dec"><span class="cl-e3ba03f2">Mean 2</span></p></th><th class="cl-e3bd51e2"><p class="cl-e3bd3dec"><span class="cl-e3ba041a">M</span><span class="cl-e3ba042e">1</span><span class="cl-e3ba03f2"> - </span><span class="cl-e3ba041a">M</span><span class="cl-e3ba042e">2</span></p></th><th class="cl-e3bd51e2"><p class="cl-e3bd3dec"><span class="cl-e3ba041a">t</span></p></th><th class="cl-e3bd51e2"><p class="cl-e3bd3dec"><span class="cl-e3ba041a">df</span></p></th><th class="cl-e3bd51e2"><p class="cl-e3bd3dec"><span class="cl-e3ba041a">p</span></p></th><th class="cl-e3bd51e2"><p class="cl-e3bd3dec"><span class="cl-e3ba03f2">95% CI</span></p></th></tr></thead><tbody><tr style="overflow-wrap:break-word;"><td class="cl-e3bd51f6"><p class="cl-e3bd3e0a"><span class="cl-e3ba03f2">Two Sample t-test</span></p></td><td class="cl-e3bd520a"><p class="cl-e3bd3dec"><span class="cl-e3ba03f2">two.sided</span></p></td><td class="cl-e3bd520a"><p class="cl-e3bd3dec"><span class="cl-e3ba03f2">654,585.37</span></p></td><td class="cl-e3bd520a"><p class="cl-e3bd3dec"><span class="cl-e3ba03f2">604,420.29</span></p></td><td class="cl-e3bd520a"><p class="cl-e3bd3dec"><span class="cl-e3ba03f2">50,165.08</span></p></td><td class="cl-e3bd520a"><p class="cl-e3bd3dec"><span class="cl-e3ba03f2">0.99</span></p></td><td class="cl-e3bd520a"><p class="cl-e3bd3dec"><span class="cl-e3ba03f2">341</span></p></td><td class="cl-e3bd520a"><p class="cl-e3bd3dec"><span class="cl-e3ba03f2">.322</span></p></td><td class="cl-e3bd520a"><p class="cl-e3bd3dec"><span class="cl-e3ba03f2">[-49287.48, 149617.63]</span></p></td></tr></tbody></table></div> ??? https://rempsyc.remi-theriault.com/articles/t-test --- # Intervalo de confianza al 95% `\begin{align*} \bar{x}_1-\bar{x}_2 &\pm t_{\alpha/2}*SE_{\bar{x_1}-\bar{x_2}} \\\\ 50165 &\pm 1.96*50561 \\\\ 50165 &\pm 99099.56 \\\\ CI[-49287.48&;149617.63] \end{align*}` Como vemos, nuestro intervalo de confianza **contiene el cero**, por lo que no se rechaza la hipótesis nula --- ## ¿Qué habría pasado con otro nivel de confianza/probabilidad de error? .medium[ ```r model3 <- t.test(salario ~ sexo, data = casen_350, var.equal=TRUE, conf.level=0.5); model3 ``` ``` Two Sample t-test data: salario by sexo t = 0.99215, df = 341, p-value = 0.3218 alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0 50 percent confidence interval: 16025.16 84304.99 sample estimates: mean in group 1 mean in group 2 654585.4 604420.3 ``` ] --- class: middle center <!-- --> --- ## Y ... qué hubiera pasado con una muestra más grande? .medium[ ```r load("casen2022_inf2.Rdata") model4 <- t.test(salario ~ sexo, data = casen2022_inf, var.equal=TRUE) model4 ``` ``` Two Sample t-test data: salario by sexo t = 22.151, df = 54754, p-value < 0.00000000000000022 alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0 95 percent confidence interval: 111554.7 133213.2 sample estimates: mean in group 1 mean in group 2 734620.3 612236.4 ``` ] --- <!-- --> --- class: inverse ## Por lo tanto, recordar: - una diferencia en la muestra puede o no puede existir en la población - para ello, establecemos una hipótesis nula (diferencias=0), que queremos rechazar - ¿cómo rechazamos? con un contraste de hipótesis, donde se establece un nivel de probabilidad de error que estamos dispuestos a aceptar - el rechazo depende tanto del nivel de probabilidad de error como también del tamaño muestral --- class: roja right .pull-left-narrow[ .left[ ### .black[Contenidos] ] ] .pull-right-wide[ ## 1- Repaso hipótesis de diferencia de medias ## .yellow[2- Hipótesis direccionales] ## 3- Hipótesis para proporciones ## 4- Inferencia en correlación ] --- # Hipótesis direccional Se siguen los mismos pasos: 1. Establecer las hipótesis (y definir si son o no direccionales) 2. Calcular error estándar 3. Estimar estadístico de prueba (ej: Z o t) 4. Establecer valor crítico de la prueba (de acuerdo a un cierto nivel de confianza) 5. Contraste e interpretación ->posibilidad de calcular intervalo de confianza --- ## Hipótesis direccional ### Paso 1: Establecimiento de hipótesis El salario de los hombres (grupo 1) es mayor al de las mujeres (grupo 2) `$$H_{a}: \bar{X}_1 \gt \bar{X}_2$$` `$$H_{0}: \bar{X}_1 \leq \bar{X}_2 0$$` --- # Paso 2 (SE) y paso 3 (Estadístico de prueba) -> son los mismos que los de las hipótesis direccionales --- ## Hipótesis direccionales ### Paso 4: Establecimiento del valor crítico de la prueba (t) .pull-left[ - para un nivel de error `\(\alpha=0.05\)` (de una cola9 - grados de libertad N-2= 343-2 = 341] .pull-right[ ```r qt(p=.05, df=341, lower.tail = FALSE) ``` ``` [1] 1.649334 ``` ] --- ## Hipótesis direccionales ### Paso 5: Contraste de hipótesis En este contraste se compara el valor estimado del estadístico de prueba y su valor crítico para una cola: `$$t{cri}= 1.64 > t{est}=0.992$$` Por lo tanto, nuestro valor estimado queda fuera de la zona de rechazo de la hipótesis nula. En consecuencia, con un nivel de confianza de 95% no podemos afirmar que el salario de los hombres es superior al de las mujeres. --- # En R ```r model5 <- t.test(salario ~ sexo, data = casen_350, alternative="greater", var.equal=TRUE, conf.level = 0.95) stats.table2 <- tidy(model5) nice_table(stats.table2, broom = "t.test") ``` <div class="tabwid"><style>.cl-e4b210a6{table-layout:auto;}.cl-e4a457f4{font-family:'Times New Roman';font-size:12pt;font-weight:normal;font-style:normal;text-decoration:none;color:rgba(0, 0, 0, 1.00);background-color:transparent;}.cl-e4a45808{font-family:'Times New Roman';font-size:12pt;font-weight:normal;font-style:italic;text-decoration:none;color:rgba(0, 0, 0, 1.00);background-color:transparent;}.cl-e4a4581c{font-family:'Times New Roman';font-size:7.2pt;font-weight:normal;font-style:normal;text-decoration:none;color:rgba(0, 0, 0, 1.00);background-color:transparent;position: relative;top:3.6pt;}.cl-e4a77506{margin:0;text-align:center;border-bottom: 0 solid rgba(0, 0, 0, 1.00);border-top: 0 solid rgba(0, 0, 0, 1.00);border-left: 0 solid rgba(0, 0, 0, 1.00);border-right: 0 solid rgba(0, 0, 0, 1.00);padding-bottom:5pt;padding-top:5pt;padding-left:5pt;padding-right:5pt;line-height: 2;background-color:transparent;}.cl-e4a77510{margin:0;text-align:left;border-bottom: 0 solid rgba(0, 0, 0, 1.00);border-top: 0 solid rgba(0, 0, 0, 1.00);border-left: 0 solid rgba(0, 0, 0, 1.00);border-right: 0 solid rgba(0, 0, 0, 1.00);padding-bottom:5pt;padding-top:5pt;padding-left:5pt;padding-right:5pt;line-height: 2;background-color:transparent;}.cl-e4a78884{background-color:transparent;vertical-align: middle;border-bottom: 0.5pt solid rgba(0, 0, 0, 1.00);border-top: 0.5pt solid rgba(0, 0, 0, 1.00);border-left: 0 solid rgba(0, 0, 0, 1.00);border-right: 0 solid rgba(0, 0, 0, 1.00);margin-bottom:0;margin-top:0;margin-left:0;margin-right:0;}.cl-e4a7888e{background-color:transparent;vertical-align: middle;border-bottom: 0.5pt solid rgba(0, 0, 0, 1.00);border-top: 0 solid rgba(0, 0, 0, 1.00);border-left: 0 solid rgba(0, 0, 0, 1.00);border-right: 0 solid rgba(0, 0, 0, 1.00);margin-bottom:0;margin-top:0;margin-left:0;margin-right:0;}.cl-e4a788a2{background-color:transparent;vertical-align: middle;border-bottom: 0.5pt solid rgba(0, 0, 0, 1.00);border-top: 0 solid rgba(0, 0, 0, 1.00);border-left: 0 solid rgba(0, 0, 0, 1.00);border-right: 0 solid rgba(0, 0, 0, 1.00);margin-bottom:0;margin-top:0;margin-left:0;margin-right:0;}</style><table data-quarto-disable-processing='true' class='cl-e4b210a6'><thead><tr style="overflow-wrap:break-word;"><th class="cl-e4a78884"><p class="cl-e4a77506"><span class="cl-e4a457f4">Method</span></p></th><th class="cl-e4a78884"><p class="cl-e4a77506"><span class="cl-e4a457f4">Alternative</span></p></th><th class="cl-e4a78884"><p class="cl-e4a77506"><span class="cl-e4a457f4">Mean 1</span></p></th><th class="cl-e4a78884"><p class="cl-e4a77506"><span class="cl-e4a457f4">Mean 2</span></p></th><th class="cl-e4a78884"><p class="cl-e4a77506"><span class="cl-e4a45808">M</span><span class="cl-e4a4581c">1</span><span class="cl-e4a457f4"> - </span><span class="cl-e4a45808">M</span><span class="cl-e4a4581c">2</span></p></th><th class="cl-e4a78884"><p class="cl-e4a77506"><span class="cl-e4a45808">t</span></p></th><th class="cl-e4a78884"><p class="cl-e4a77506"><span class="cl-e4a45808">df</span></p></th><th class="cl-e4a78884"><p class="cl-e4a77506"><span class="cl-e4a45808">p</span></p></th><th class="cl-e4a78884"><p class="cl-e4a77506"><span class="cl-e4a457f4">95% CI</span></p></th></tr></thead><tbody><tr style="overflow-wrap:break-word;"><td class="cl-e4a7888e"><p class="cl-e4a77510"><span class="cl-e4a457f4">Two Sample t-test</span></p></td><td class="cl-e4a788a2"><p class="cl-e4a77506"><span class="cl-e4a457f4">greater</span></p></td><td class="cl-e4a788a2"><p class="cl-e4a77506"><span class="cl-e4a457f4">654,585.37</span></p></td><td class="cl-e4a788a2"><p class="cl-e4a77506"><span class="cl-e4a457f4">604,420.29</span></p></td><td class="cl-e4a788a2"><p class="cl-e4a77506"><span class="cl-e4a457f4">50,165.08</span></p></td><td class="cl-e4a788a2"><p class="cl-e4a77506"><span class="cl-e4a457f4">0.99</span></p></td><td class="cl-e4a788a2"><p class="cl-e4a77506"><span class="cl-e4a457f4">341</span></p></td><td class="cl-e4a788a2"><p class="cl-e4a77506"><span class="cl-e4a457f4">.161</span></p></td><td class="cl-e4a788a2"><p class="cl-e4a77506"><span class="cl-e4a457f4">[-33228.46, Inf]</span></p></td></tr></tbody></table></div> --- <!-- --> --- class: roja right .pull-left-narrow[ .left[ ### .black[Contenidos] ] ] .pull-right-wide[ ## 1- Repaso hipótesis de diferencia de medias ## 2- Hipótesis direccionales ## .yellow[3- Hipótesis para proporciones] ## 4- Inferencia en correlación ] --- # Test para proporciones - además de las inferencias con medidas de tendencia central (como promedios), es posible también realizar inferencia sobre porcentajes/proporciones, ej: - El 20% de l_s chilen_s asiste a la educación superior (hipótesis puntual) - Los hombres y las mujeres tienen un distinto porcentaje de acceso a la educación superior (hipótesis de diferencia) - Las mujeres asisten más a la educación superior que los hombres (hipótesis direccional) --- # Datos ```r stargazer(as.data.frame(casen2022_inf), type = "text") ``` ``` ========================================================= Statistic N Mean St. Dev. Min Max --------------------------------------------------------- salario 54,756 680,138.000 645,405.500 8,000 25,000,000 sexo 57,530 1.445 0.497 1 2 educacion 57,530 10.350 2.245 1 15 --------------------------------------------------------- ``` --- .small[ ```r frq(casen2022_inf$educacion) ``` ``` e6a_no_asiste. ¿Cuál es el nivel educacional más alto al cual asistió? (x) <numeric> # total N=57530 valid N=57530 mean=10.35 sd=2.25 Value | Label | N | Raw % | Valid % | Cum. % ------------------------------------------------------------------------------------------------------------ 1 | 1. Nunca asistió | 242 | 0.42 | 0.42 | 0.42 2 | 2. Sala cuna | 0 | 0.00 | 0.00 | 0.42 3 | 3. Jardín Infantil (Medio menor y Medio mayor) | 3 | 0.01 | 0.01 | 0.43 4 | 4. Prekínder / Kínder (Transición menor y Transición Mayor) | 4 | 0.01 | 0.01 | 0.43 5 | 5. Educación Especial (Diferencial) | 73 | 0.13 | 0.13 | 0.56 6 | 6. Primaria o Preparatoria (Sistema antiguo) | 472 | 0.82 | 0.82 | 1.38 7 | 7. Educación Básica | 7728 | 13.43 | 13.43 | 14.81 8 | 8. Humanidades (Sistema Antiguo) | 348 | 0.60 | 0.60 | 15.42 9 | 9. Educación Media Científico-Humanista | 18879 | 32.82 | 32.82 | 48.23 10 | 10. Técnica, Comercial, Industrial o Normalista (Sistema Antiguo) | 280 | 0.49 | 0.49 | 48.72 11 | 11. Educación Media Técnica Profesional | 7457 | 12.96 | 12.96 | 61.68 12 | 12. Técnico Nivel Superior (Carreras 1 a 3 años) | 7623 | 13.25 | 13.25 | 74.93 13 | 13. Profesional (Carreras 4 o más años) | 13166 | 22.89 | 22.89 | 97.82 14 | 14. Magíster o maestría | 1098 | 1.91 | 1.91 | 99.73 15 | 15. Doctorado | 157 | 0.27 | 0.27 | 100.00 <NA> | <NA> | 0 | 0.00 | <NA> | <NA> ``` ] --- ###Generar variable educación universitaria y menos que universitaria: .medium[ ```r casen2022_inf$educ_sup <- rec(casen2022_inf$educacion, rec = "1:12=0;13:15=1",val.labels = c("Menos que universitaria", "Universitaria o más")) frq(casen2022_inf$educ_sup) ``` ``` e6a_no_asiste. ¿Cuál es el nivel educacional más alto al cual asistió? (x) <numeric> # total N=57530 valid N=57530 mean=0.25 sd=0.43 Value | Label | N | Raw % | Valid % | Cum. % ------------------------------------------------------------------ 0 | Menos que universitaria | 43109 | 74.93 | 74.93 | 74.93 1 | Universitaria o más | 14421 | 25.07 | 25.07 | 100.00 <NA> | <NA> | 0 | 0.00 | <NA> | <NA> ``` ] --- .pull-left[ .small[ ```r pacman::p_load(sjPlot) casen2022_inf %>% sjtab(educ_sup,sexo, show.col.prc=TRUE) ``` <table style="border-collapse:collapse; border:none;"> <tr> <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal; border-bottom:1px solid;" rowspan="2">e6a_no_asiste. ¿Cuál<br>es el nivel<br>educacional más alto<br>al cual asistió?</th> <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal;" colspan="2">Sexo</th> <th style="border-top:double; text-align:center; font-style:italic; font-weight:normal; font-weight:bolder; font-style:italic; border-bottom:1px solid; " rowspan="2">Total</th> </tr> <tr> <td style="border-bottom:1px solid; text-align:center; padding:0.2cm;">1. Hombre</td> <td style="border-bottom:1px solid; text-align:center; padding:0.2cm;">2. Mujer</td> </tr> <tr> <td style="padding:0.2cm; text-align:left; vertical-align:middle;">Menos que<br>universitaria</td> <td style="padding:0.2cm; text-align:center; "><span style="color:black;">25102</span><br><span style="color:#339933;">78.6&nbsp;&#37;</span></td> <td style="padding:0.2cm; text-align:center; "><span style="color:black;">18007</span><br><span style="color:#339933;">70.3&nbsp;&#37;</span></td> <td style="padding:0.2cm; text-align:center; "><span style="color:black;">43109</span><br><span style="color:#339933;">74.9&nbsp;&#37;</span></td> </tr> <tr> <td style="padding:0.2cm; text-align:left; vertical-align:middle;">Universitaria o más</td> <td style="padding:0.2cm; text-align:center; "><span style="color:black;">6818</span><br><span style="color:#339933;">21.4&nbsp;&#37;</span></td> <td style="padding:0.2cm; text-align:center; "><span style="color:black;">7603</span><br><span style="color:#339933;">29.7&nbsp;&#37;</span></td> <td style="padding:0.2cm; text-align:center; "><span style="color:black;">14421</span><br><span style="color:#339933;">25.1&nbsp;&#37;</span></td> </tr> <tr> <td style="padding:0.2cm; border-bottom:double; font-weight:bolder; font-style:italic; text-align:left; vertical-align:middle;">Total</td> <td style="padding:0.2cm; text-align:center; border-bottom:double;"><span style="color:black;">31920</span><br><span style="color:#339933;">100&nbsp;&#37;</span></td> <td style="padding:0.2cm; text-align:center; border-bottom:double;"><span style="color:black;">25610</span><br><span style="color:#339933;">100&nbsp;&#37;</span></td> <td style="padding:0.2cm; text-align:center; border-bottom:double;"><span style="color:black;">57530</span><br><span style="color:#339933;">100&nbsp;&#37;</span></td> </tr> <td style="text-align:right; font-size:0.9em; font-style:italic; padding:0.2cm;" colspan="4">&chi;²=524.222 &middot; df=1 &middot; &phi;=0.095 &middot; p=0.000</td> </tr> </table> ]] .pull-right[ <br> <br> `\(p_m - p_h=0.297-0.214=0.083\)` El porcentaje de mujeres con educación universitaria es .red[8.3%] superior en las mujeres <br> .content-box-red[.center[ .red[¿Es significativa esta diferencia?] ] ] ] ??? ver: http://www.sthda.com/english/wiki/two-proportions-z-test-in-r --- # Diferencias entre proporciones 1. Establecer las hipótesis (y definir si son o no direccionales) 2. Calcular error estándar 3. Estimar estadístico de prueba (ej: Z o t) 4. Establecer valor crítico de la prueba (de acuerdo a un cierto nivel de confianza) 5. Contraste e interpretación ->posibilidad de calcular intervalo de confianza --- ## Diferencias entre proporciones ### 1. Establecer las hipótesis ¿Existen diferencias entre el porcentaje de mujeres y hombres con nivel educacional universitario? `$$H_{a}: p_{mujeres} - p_{hombres} \neq 0$$` `$$H_{0}: p_{mujeres} - p_{hombres}= 0$$` --- ## Diferencias entre proporciones ### 2. Cálculo de error estándar Recordemos que el SE para una proporción es: $$SE_p=\sqrt{\frac{p(1-p)}{n}} $$ Y para diferencia de proporciones: `$$SE_{p_1 - p_2}=\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}$$` ??? https://online.stat.psu.edu/stat415/lesson/9/9.4 --- Estimación de error estándar `\begin{align*} SE_{p_a - p_b}&=\sqrt{\frac{p_a(1-p_a)}{n_a}+\frac{p_b(1-p_b)}{n_b}} \\\\ SE_{p_m - p_h}&=\sqrt{\frac{0.297(1-0.297)}{7603}+\frac{0.214(1-0.214)}{6818}} \\\\ SE_{p_m - p_h}&=\sqrt{\frac{0.209}{7603}+\frac{0.168}{6818}}=\sqrt{0.0000275+0.0000246}=0.00722 \end{align*}` --- ## Diferencias entre proporciones ### 3. Cálculo de estadístico de prueba Para diferencia de proporciones también se utiliza la prueba `\(Z\)` `$$Z_{est}=\frac{p_m - p_h}{SE_{p_m -p_h}}=\frac{0.083}{0.0072}=11.528$$` --- ## Diferencias entre proporciones ### 4. Establecer valor crítico de prueba Y comparamos este valor con el Z crítico para un `\(\alpha=0.05\)` de dos colas (porque es hipótesis de diferencia) ```r qnorm(p=.05/2, lower.tail=FALSE) ``` ``` [1] 1.959964 ``` --- ## Diferencias entre proporciones ### 5. Interpretación En este caso, nuestro `\(Z_{est}=11.528\)` > `\(Z_{cri}=1.96\)`, por lo tanto se rechaza `\(H_0\)` La proporción de universitarias y universitarios es diferente, con un 95% de confianza --- ## (6). Construcción intervalo de confianza .medium[ Para obtener un intervalo de confianza, a la diferencia de proporciones se le suman/restan errores estándar muttiplicados por el valor Z crítico según nivel de confianza, en este caso `\(\alpha=0.5/2\)` (prueba de dos colas) `\begin{align*} p_1 - p_2 &\pm Z_{crit_{\alpha/2}}*SE_{p_a - p_b} \\ 0.297-0.214 &\pm1.96*0.00722\\ 0.083&\pm 0.0142 \\ \end{align*}` `$$CI[0.07;0.09]$$` Podemos entonces decir con un 95% de confianza que la diferencia de proporción de universitari_s entre hombres y mujeres se encuentra entre un 7% y un 9%] --- # Estimación directamente en R con .blue[prop.test] .small[ .pull-left[ ```r prop_dif <-prop.test(x = c(7603,6818), n = c(25610,31920)) prop_dif ``` 2-sample test for equality of proportions with continuity correction data: c(7603, 6818) out of c(25610, 31920) X-squared = 524.22, df = 1, p-value < 0.00000000000000022 alternative hypothesis: two.sided 95 percent confidence interval: 0.07606640 0.09049306 sample estimates: prop 1 prop 2 0.2968762 0.2135965 ] ] .pull-right[ .medium[ Dos cosas importantes para reporte de este output: - probabilidad de error p: si es menor al nivel de error especificado ( `\(\alpha\)`), se rechaza la hipótesis nula. En este caso, las diferencias entre grupos son significativamente distinas de cero. - el intervalo de confianza: rango de valores con un 95% de confianza para la diferencia estimada. ] ] ??? --- ## Hipótesis direccionales de proporciones ### Paso 1: hipótesis ¿Es superior la proporción de mujeres con educación superior? En este caso, `$$H_{0}: p_{mujeres} \leq p_{hombres}$$` En relación a la siguiente hipótesis alternativa: `$$H_{a}: p_{mujeres} \gt p_{hombres}$$` --- ## Hipótesis direccionales de proporciones ### Paso 2 (SE) y 3 (estadístico de prueba) igual que para hipótesis no direccionales --- ## Hipótesis direccionales de proporciones ### Paso 4: Valor crítico de prueba Valor crítico de Z para una cola ```r qnorm(p=.05, lower.tail=FALSE) ``` ``` [1] 1.644854 ``` --- ## Hipótesis direccionales de proporciones ### Paso 5: Interpretación Valor crítico se compara con el valor estimado de Z para la diferencia de proporciones, En este caso, `$$Z_{est}=11.528 \gt Z_{cri}=1.644$$` Por lo tanto se rechaza `\(\H_0\)`, con un 95% de confianza podemos decir que la proporción de mujeres universitarias es mayor en mujeres que en hombres. --- # Estimación directamente en R con .blue[prop.test] .small[ .pull-left[ ```r prop_greater <-prop.test(x = c(7603,6818), n = c(25610,31920), alternative = "greater") prop_greater ``` ``` 2-sample test for equality of proportions with continuity correction data: c(7603, 6818) out of c(25610, 31920) X-squared = 524.22, df = 1, p-value < 0.00000000000000022 alternative hypothesis: greater 95 percent confidence interval: 0.07722045 1.00000000 sample estimates: prop 1 prop 2 0.2968762 0.2135965 ``` ] ] .pull-right[ .medium[ ] ] --- class: roja right .pull-left-narrow[ .left[ ### .black[Contenidos] ] ] .pull-right-wide[ ## 1- Repaso hipótesis de diferencia de medias ## 2- Hipótesis direccionales ## 3- Hipótesis para proporciones ## .yellow[4- Inferencia en correlación] ] --- # Datos .medium[ Simulamos dos variables: edad, y puntaje en escala de izquierda (1) - derecha (10): ```r edad <-c(18,25,40,55,70, 82) iz_der <-c(5,4,5,9,5,7) cor(edad,iz_der) ``` ``` [1] 0.5070278 ``` ```r (cor(edad,iz_der))^2 #r2 ``` ``` [1] 0.2570772 ``` ] --- .pull-left[ ```r plot1 <- ggplot(, aes(x=edad, y=iz_der)) + geom_point( colour = "red", size = 5) + theme(text = element_text(size = 20)) ``` ] .pull-right[ ```r plot1 ``` <!-- --> ] --- ## Prueba de hipótesis de correlación ### 1. Formulación de hipótesis Siendo `\(\rho\)` (rho) la correlación `\(r\)` en la población: `$$H_0: \rho = 0$$` `$$H_a: \rho \neq 0$$` --- ## Prueba de hipótesis de correlación ### 2. Error estándar de la correlación `\begin{align*} SE_r=&\sqrt{\frac{1-r²}{n-2}} \\\\ =&\sqrt{\frac{1-0.257}{6-2}} \\\\ =&\sqrt{\frac{0.743}{4}}=\sqrt{0.186}=0.431 \end{align*}` --- ## Prueba de hipótesis de correlación ### 3. Estimación de estadístico de prueba ( `\(t\)`) `\begin{align*} t_r&=\frac{r}{SE_r} \\\\ &=\frac{0.51}{0.431} \\\\ &=1.18 \end{align*}` --- ## Prueba de hipótesis de correlación ### 4. Valor crítico para `\(t\)` .pull-left[ - para un nivel de error `\(\alpha=0.05\)` - y una hipótesis de diferencia de dos colas: `\(\alpha/2=[0.025-0.975]\)` - grados de libertad N-2= 6-2 = 4] .pull-right[ ```r qt(p=.05/2, df=4, lower.tail=FALSE) ``` ``` [1] 2.776445 ``` ] --- ## Prueba de hipótesis de correlación ### 5. Interpretación `\(t_{r}=1.18 < t_{cri}=2.77\)` Nuestro t estimado es menor que el valor t crítico para un 95% de confianza, por lo tanto no rechazamos la hipótesis nula. No existe evidencia en nuestros datos para afirmar que la correlación entre la escala izquierda-derecha y edad es distinta de cero en la población. --- ## En R ```r cor.test(iz_der,edad) ``` ``` Pearson's product-moment correlation data: iz_der and edad t = 1.1765, df = 4, p-value = 0.3046 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: -0.5174601 0.9341863 sample estimates: cor 0.5070278 ``` --- <!-- --> --- class: inverse ## Resumen - 5 pasos en la prueba de hipótesis - Hipótesis direccionales y no direccionales - Hipótesis para - estimación puntual (ej: correlación) - diferencias - comparación --- # ASISTENCIA .pull-left[  ] .pull-right[ <br> <br> <br> <br> <br> bit.ly/correlacional-asistencia ] --- class: front .pull-left-wide[ # Estadística Correlacional] .pull-right-narrow[] ## Asociación, inferencia y reporte ---- .pull-left[ ## Juan Carlos Castillo ## Sociología FACSO - UChile ## 2do Sem 2023 ## [.orange[correlacional.netlify.com]](https://encuestas-sociales.netlify.com) ]