Cálculo y reporte de correlación

Completar hasta as 11:59 PM del viernes, 25 de agosto de 2023

Objetivo de la práctica

El objetivo de esta guía práctica es aprender a calcular y graficar la correlación entre dos variables utilizando R.

En detalle, aprenderemos:

Qué es una correlación
Cuál es la correlación de Pearson
Cómo calcular una correlación de Pearson y graficarla

1. Qué es la Correlación

La correlación es una medida estadística que describe la asociación entre dos variables. Cuando existe correlación entre dos variables, el cambio en una de ellas tiende a estar asociado con un cambio en la otra variable.

En términos concretos, lo que observamos es cómo se comportan los valores de dos (o más) variables para cada observación, y si podemos suponer que ese comportamiento conjunto tiene algún patrón.

2. Correlación de Pearson

La correlación de Pearson (o coeficiente de correlación de pearson) es una medida estadística que cuantifica la relación lineal entre dos variables continuas. Esta medida va desde -1 hasta 1, donde:

r=1: Correlación positiva perfecta. Cuando una variable aumenta, la otra también aumenta en proporción constante.
r=−1: Correlación negativa perfecta. Cuando una variable aumenta, la otra disminuye en proporción constante.
r=0: No hay correlación lineal entre las variables. No hay una relación lineal discernible entre los cambios en las variables.

Cuanto más cercano esté el valor de r a 1 o -1, más fuerte será la correlación. Cuanto más cercano esté a 0, más débil será la correlación.

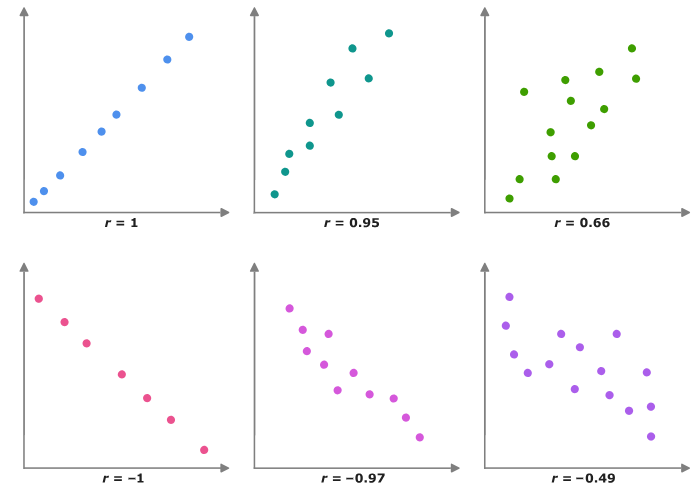
En el siguiente enlace pueden visualizar la correlación para dos variables cambiando la fuerza y el sentido de esta, al mismo tiempo que les permite observar la varianza compartida entre ambas variables.

3. Estimación de la correlación de Pearson

Utilizaremos un set mínimo simulado de datos (el mismo de la sesión 3 )

Simulamos datos para 8 casos

con 8 niveles de educación (ej: desde basica incompleta=1, hasta postgrado=8), y
12 niveles de rangos de ingreso (ej: desde menos de 100.000=1 hasta más de 10.000.000=12)

id <-seq(1,8) # identificador de cada caso
educ <- c(2,3,4,4,5,7,8,8)
ing  <- c(1,3,3,5,4,7,9,11)
data <- data.frame(id,educ,ing)

kableExtra::kbl(data, escape=F, full_width = F)  %>%
   kable_paper("hover")

id	educ	ing
1	2	1
2	3	3
3	4	3
4	4	5
5	5	4
6	7	7
7	8	9
8	8	11

La correlación de Pearson se basa en la covarianza, que es una medida de asociación entre variables basada en la varianza de cada una de ellas:

\[\begin{align*} Covarianza = cov(x,y) &= \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {n-1}\\ \\ Correlación=r &= \frac{\sum_{i=1}^{n}(x_i - \bar{x})(y_i - \bar{y})} {(n-1)\sigma_x \sigma_y }\\ \\ &= \frac{\sum(x-\bar{x})(y-\bar{y})}{\sqrt{\sum(x-\bar{x})^{2} \sum(y-\bar{y})^{2}}} \end{align*}\]

Para obtener el coeficiente de correlación directamente en R se utiliza la función cor() :

cor(data$educ, data$ing)

[1] 0.9512367

Vamos por paso:

\((x_i - \bar{x})\) es la diferencia de un valor de una variable respecto de su promedio. Por ejemplo, si x=educación, y un caso tiene educación 6 y el promedio de educación es 2, entonces el valor de \((x_i - \bar{x})=4\)
\((y_i - \bar{y})\) : lo mismo pero para la otra varible, en el caso de nuestro ejemplo es ingreso.
\((x-\bar{x})(y-\bar{y})\) es la multiplicación de los dos pasos anteriores para cada caso.
\(\sum(x-\bar{x})(y-\bar{y})\) es la suma de estos valores para el total de los casos

En nuestra base de datos de ejemplo simulamos columnas adicionales con esta información:

\((x_i - \bar{x})\) : dif_m_educ
\((y_i - \bar{y})\) : dif_m_ing
\((x-\bar{x})(y-\bar{y})\) : dif_xy

Y además las diferencias de promedio de cada variable al cuadrado:

\((x_i - \bar{x})²\) : dif_m_educ2
\((y_i - \bar{y})²\) : dif_m_ing2

data$dif_m_educ <- data$educ-mean(data$educ)
data$dif_m_ing <- data$ing-mean(data$ing)
data$dif_xy <-  data$dif_m_educ*data$dif_m_ing
data$dif_m_educ2 <- (data$dif_m_educ)^2
data$dif_m_ing2 <- (data$dif_m_ing)^2

En nuestra base de datos:

kableExtra::kbl(data, digits = 3,full_width = F)  %>%
   kable_paper("hover")

id	educ	ing	dif_m_educ	dif_m_ing	dif_xy	dif_m_educ2	dif_m_ing2
1	2	1	-3.125	-4.375	13.672	9.766	19.141
2	3	3	-2.125	-2.375	5.047	4.516	5.641
3	4	3	-1.125	-2.375	2.672	1.266	5.641
4	4	5	-1.125	-0.375	0.422	1.266	0.141
5	5	4	-0.125	-1.375	0.172	0.016	1.891
6	7	7	1.875	1.625	3.047	3.516	2.641
7	8	9	2.875	3.625	10.422	8.266	13.141
8	8	11	2.875	5.625	16.172	8.266	31.641

Y obtenemos la suma de cada una de las tres últimas columnas, que es lo que se necesita para reemplazar en la fórmula de la correlación:

sum(data$dif_xy); sum(data$dif_m_educ2);sum(data$dif_m_ing2)

[1] 51.625

[1] 36.875

[1] 79.875

Reemplazando,

\[\begin{align*} r &= \frac{\sum(x-\bar{x})(y-\bar{y})}{\sqrt{\sum(x-\bar{x})^{2} \sum(y-\bar{y})^{2}}} \\ \\ &= \frac{51.625}{ \sqrt{36.875*79.875}} \\ \\ &= \frac{51.625}{54.271} \\ \\ &= 0.951 \end{align*}\]

Y comprobamos con la función cor() de R, que nos entrega la correlación de Pearson:

cor(data$educ, data$ing)

[1] 0.9512367

Como vimos en clases, el valor de la correlación va entre -1 y 1, donde el valor 0 significa que las dos variables no se encuentran correlacionadas, y el valor -1 y 1 significa que se encuentran completamente correlacionadas, positiva y negativamente, respectivamente.

En este caso, un valor de 0.95 es muy alto, y significa que las variables ingreso y educación, en nuestra base de datos simulada, se encuentran fuertemente correlacionadas.

Diagrama de dispersión (nube de puntos o scatterplot)

Siempre es recomendable acompañar el valor de la correlación con una exploración gráfica de la distribución bivariada de los datos. El gráfico o diagrama de dispersión es una buena herramienta, ya que muestra la forma, la dirección y la fuerza de la relación entre dos variables cuantitativas.

Este tipo de gráfico lo podemos realizar usando la librería ggplot2.

pacman::p_load(ggplot2)
plot1 <- ggplot(data, 
                aes(x=educ, y=ing)) + 
                geom_point(colour = "red", 
                size = 5)
plot1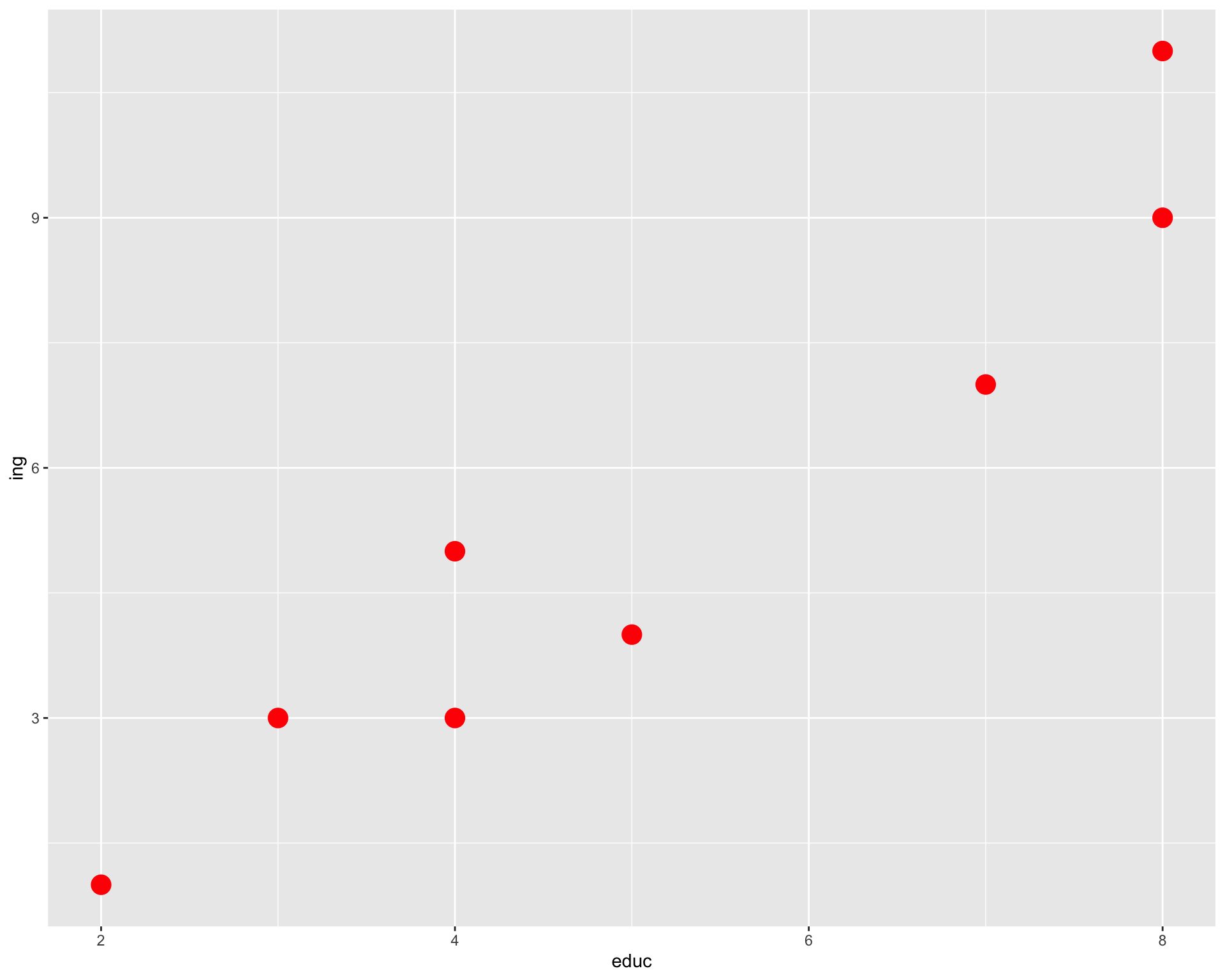

En el gráfico podemos ver como se crea una nube de puntos en las intersecciones de los valores para ambas variables de cada caso.

El cuarteto de Anscombe y las limitaciones de la correlación lineal

Ahora, revisaremos un muy buen ejemplo de la importancia de la exploración gráfica de los datos mediante un ejemplo de Anscombe (1973), que permite visualizar las limitaciones del coeficiente de correlación.

Primero, crearemos la base de datos:

anscombe <- data.frame(
  x1 = c(10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5),
  y1 = c(8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.82, 5.68),
  x2 = c(10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5),
  y2 = c(9.14, 8.14, 8.74, 8.77, 9.26, 8.10, 6.13, 3.10, 9.13, 7.26, 4.74),
  x3 = c(10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5),
  y3 = c(7.46, 6.77, 12.74, 7.11, 7.81, 8.84, 6.08, 5.39, 8.15, 6.42, 5.73),
  x4 = c(8, 8, 8, 8, 8, 8, 8, 19, 8, 8, 8),
  y4 = c(6.58, 5.76, 7.71, 8.84, 8.47, 7.04, 5.25, 12.50, 5.56, 7.91, 6.89)
)

Calculamos la correlación pares de datos

cor(anscombe$x1, anscombe$y1)

[1] 0.8164205

cor(anscombe$x2, anscombe$y2)

[1] 0.8162365

cor(anscombe$x3, anscombe$y3)

[1] 0.8162867

cor(anscombe$x4, anscombe$y4)

[1] 0.8165214

Podemos observar que los valores de las correlaciones son equivalentes, por lo tanto podríamos pensar que todos los pares de columnas se encuentran correlacionados de manera similar.

Pero, ¿será suficiente con esa información? Pasemos a revisar los gráficos de dispersión de cada par de variables.

ggplot(anscombe, aes(x = x1, y = y1)) +
  geom_point(colour = "red", 
             size = 5) +
  geom_smooth(method = "lm", se = FALSE, color="blue", size=0.5) +
  labs(title = "Caso I")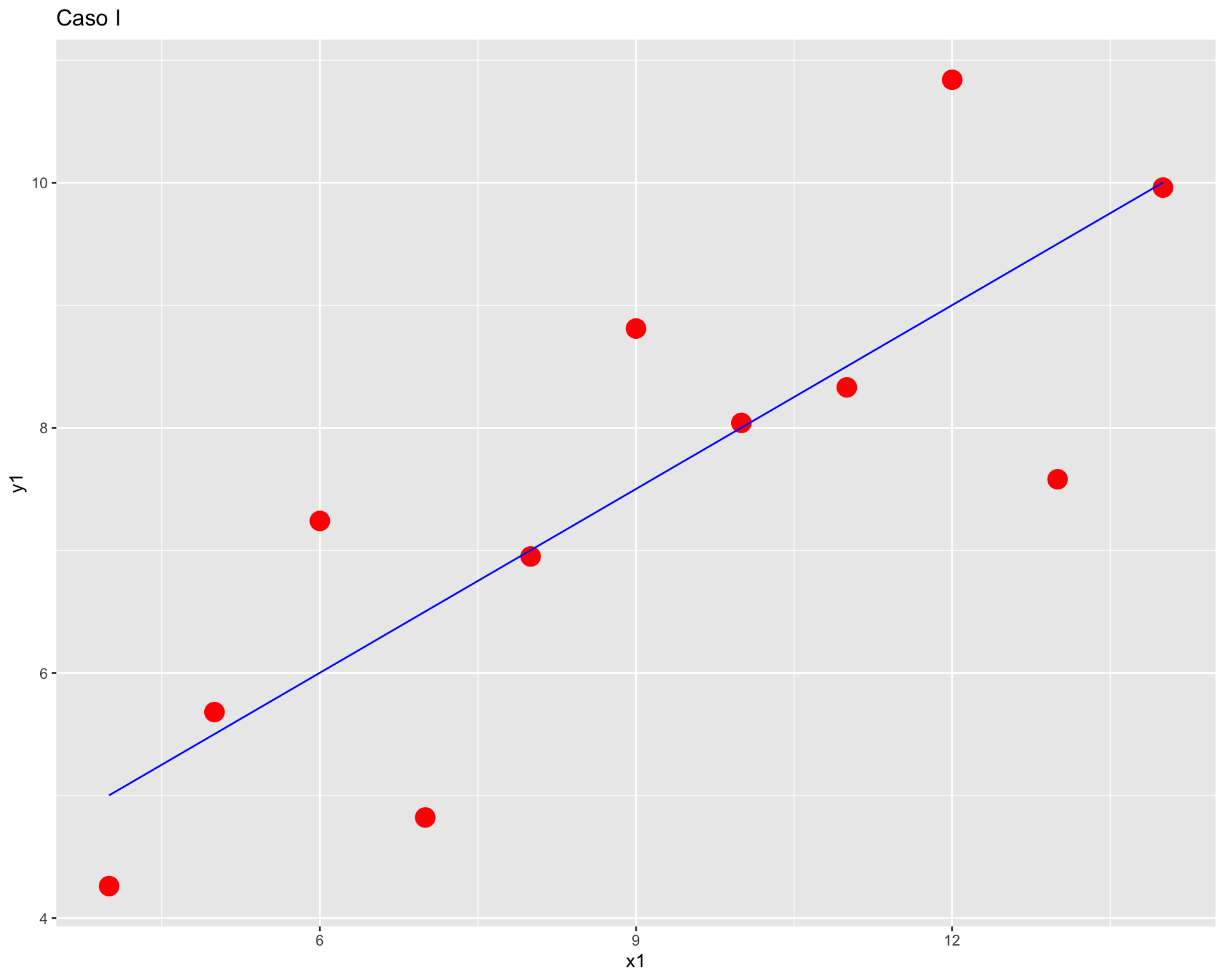

ggplot(anscombe, aes(x = x2, y = y2)) +
  geom_point(colour = "green", 
             size = 5) +
  geom_smooth(method = "lm", se = FALSE, color="blue", size=0.5) +
  labs(title = "Caso II")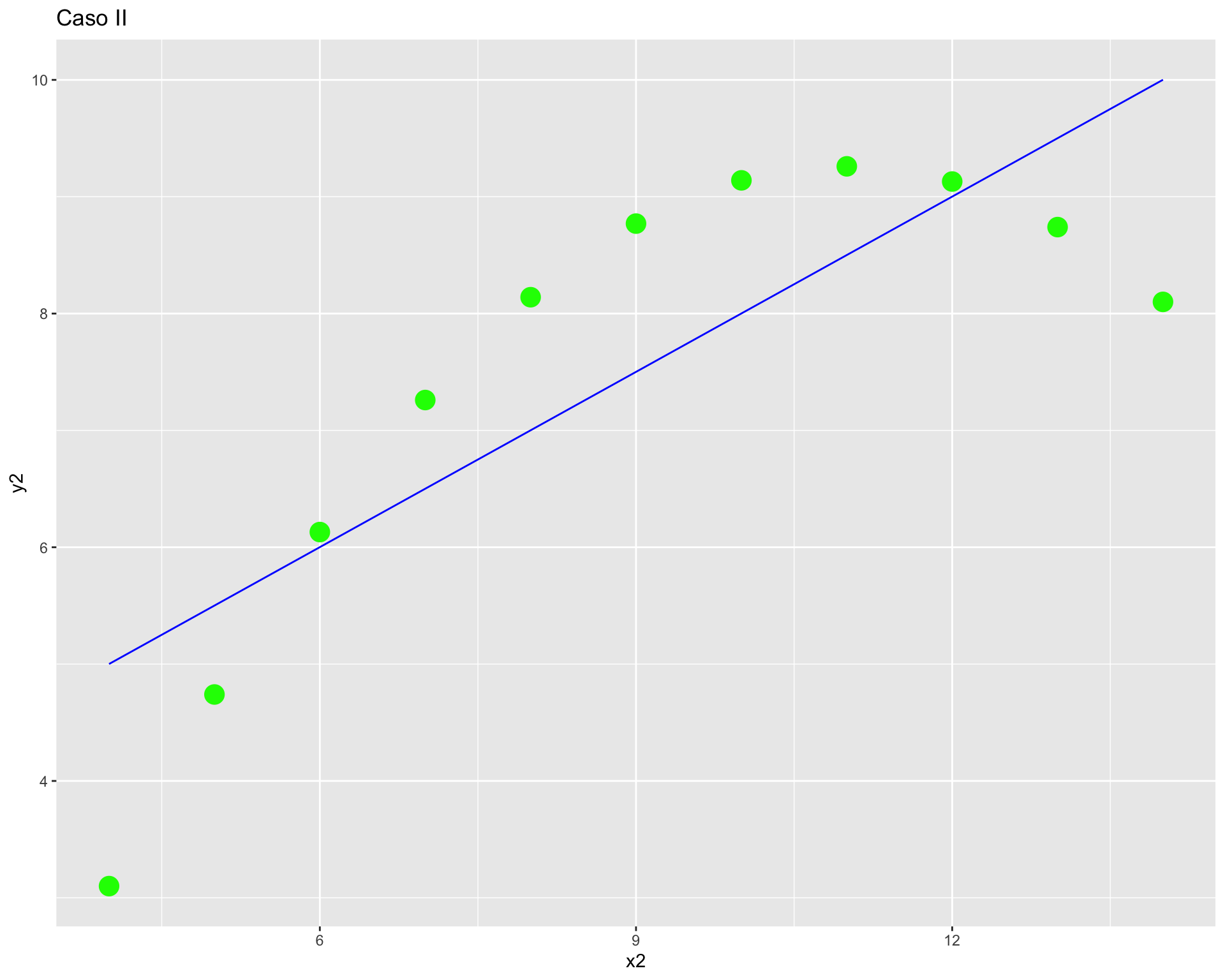

ggplot(anscombe, aes(x = x3, y = y3)) +
  geom_point(colour = "yellow", 
             size = 5) +
  geom_smooth(method = "lm", se = FALSE, color="blue", size=0.5) +
  labs(title = "Caso III")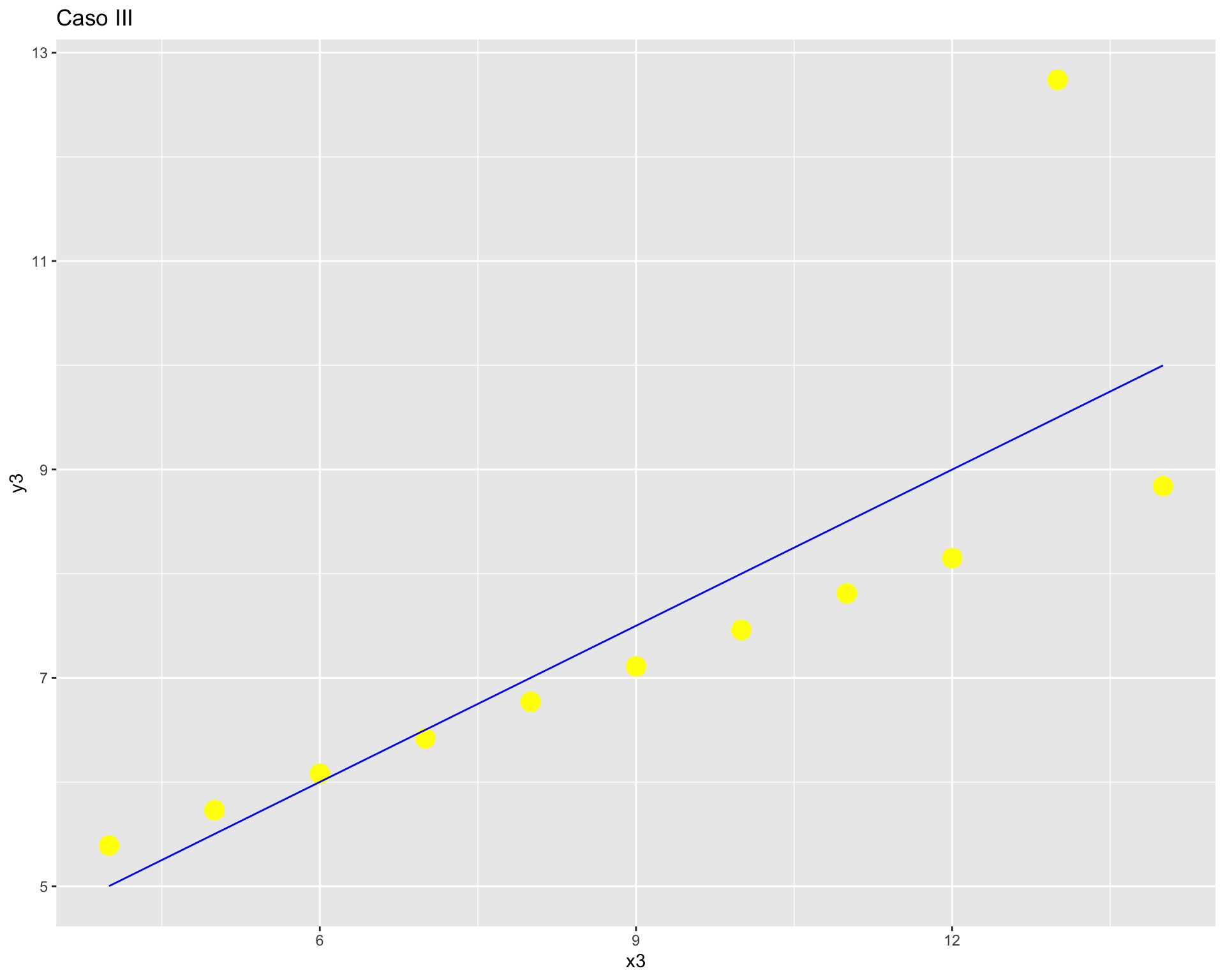

ggplot(anscombe, aes(x = x4, y = y4)) +
  geom_point(colour = "orange", 
             size = 5) +
  geom_smooth(method = "lm", se = FALSE, color="blue", size=0.5) +
  labs(title = "Caso IV")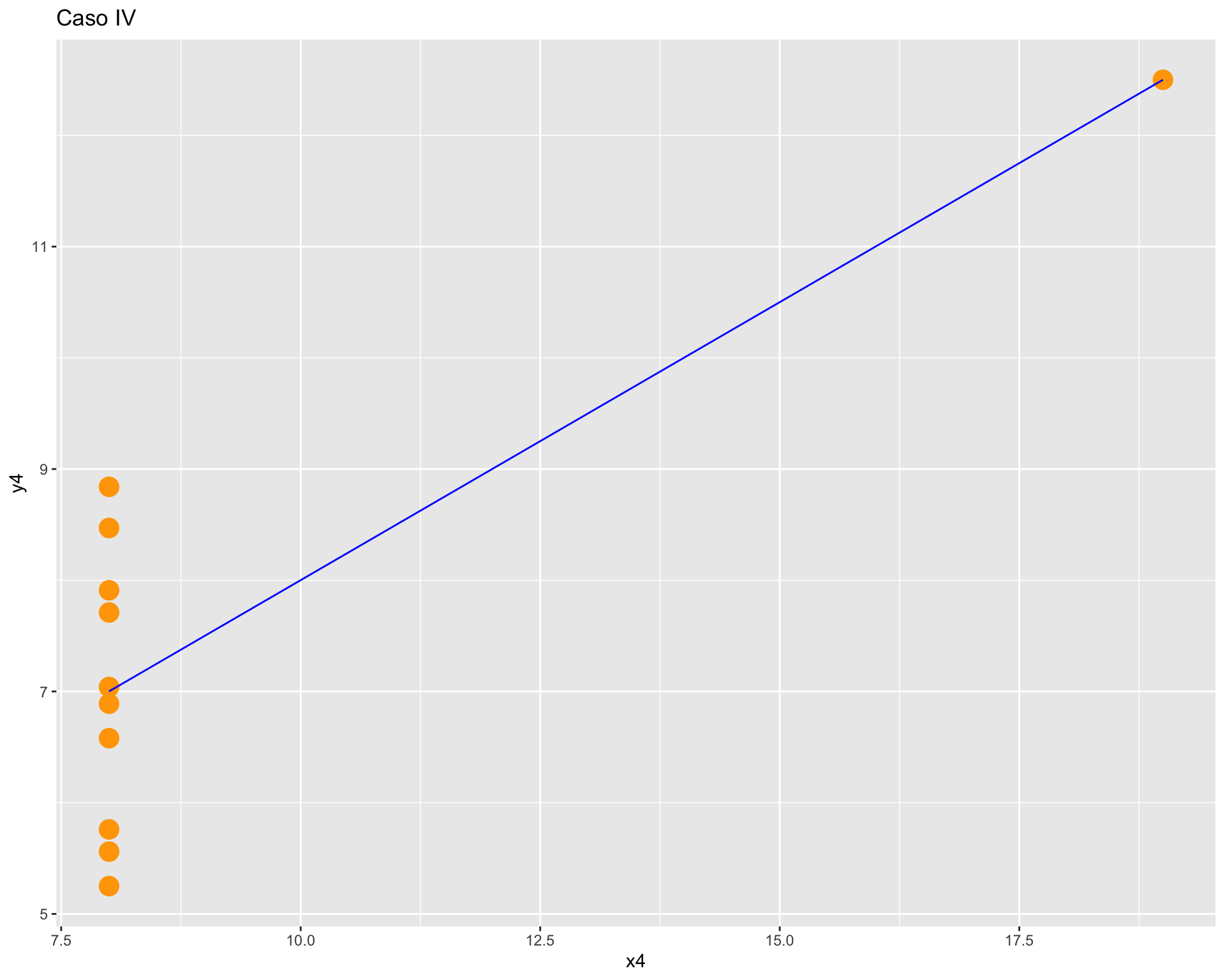

Como vemos, con distintas distribuciones las correlaciones pueden ser las mismas, principalmente porque Pearson es una medida que solo captura relaciones lineales (rectas), además de verse influido fuertemente por valores extremos. Por lo mismo, es relevante siempre una buena visualización de la distribución bivariada de los datos como complemento al cálculo del coeficiente de correlación.

Reporte de progreso

Completar el reporte de progreso correspondiente a esta práctica aquí. El plazo para contestarlo es hasta el día viernes de la semana en la que se publica la práctica correspondiente.