x.values <- seq(-4,4, length = 1000)
y.values <- dnorm(x.values)
plot(x.values, y.values, type="l", xlab="Z value", ylab="Probability", main="Normal Distribution")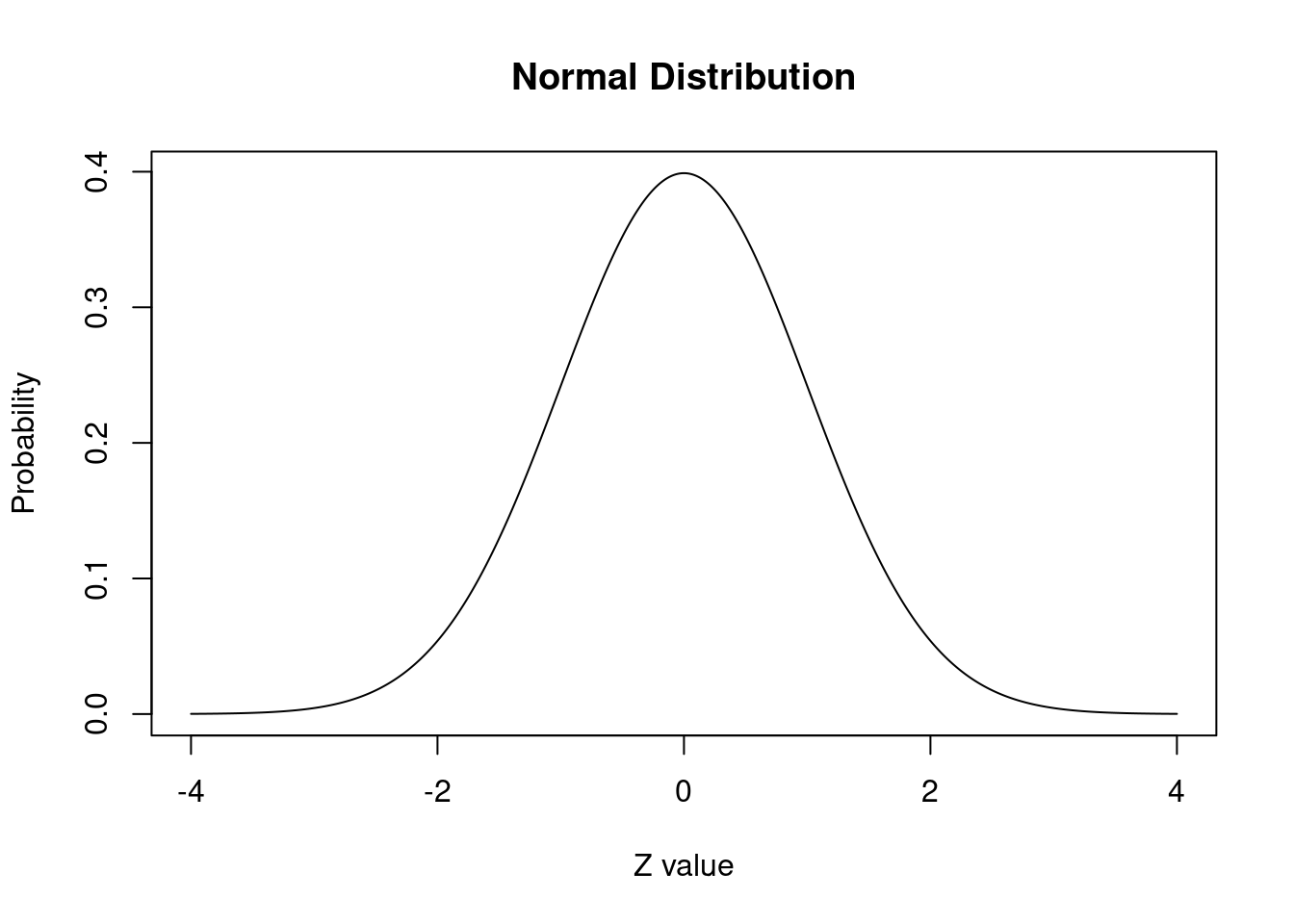
Inferencia 1: Curva normal
Completar hasta as 11:59 PM del viernes, 8 de septiembre de 2023
Objetivo de la práctica
El objetivo de esta guía práctica es introducirnos en la inferencia estadística, revisando los conceptos y aplicaciones de la curva normal y las probabilidades bajo esta con puntajes Z.
En detalle, aprenderemos:
- Qué es la inferencia estadística.
- Qué es la distribución normal y cómo interpretarla.
- Cómo calcular probabilidades asociadas con valores Z en R.
¿Qué es la inferencia estadística?
En estadística, llamamos inferencia al ejercicio de extrapolar determinadas estimaciones (estadístico) de una muestra a una población más grande (parámetro). En concreto, es el proceso de realizar conclusiones o predicciones sobre una población a partir de una muestra o subconjunto de esa población.
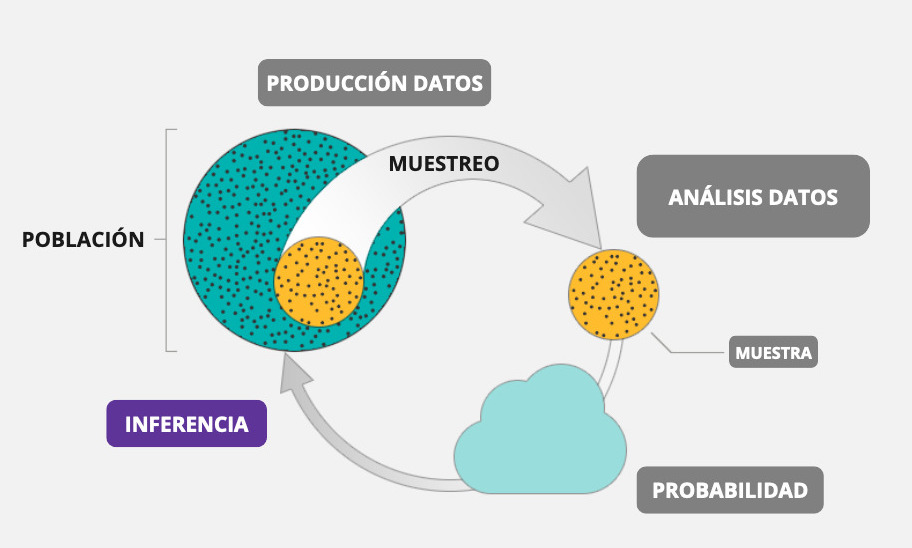
Un concepto central en todo esto es la probabilidad de error, es decir, en qué medida nos estamos equivocando (o estamos dispuestos a estar equivocados) en tratar de extrapolar una estimación muestral a la población.
Distribución normal
Nota
Recordemos que por distribución nos referimos al conjunto de todos los valores posibles de una variable y las frecuencias (o probabilidades) con las que se producen.
Existen distribuciones empíricas y distribuciones teóricas, en donde:
- las primeras reflejan la distribución de los valores que asume la variable en un grupo concreto a partir de una observación.
- las segundas son una función matématica que expresan la distribución de un conjunto de números mediante su probabilidad de ocurencia.
Para empezar, veamos una de las distribuciones teóricas más conocidas: la distribución normal estándar. La distribución normal estándar:
- es una distribución normal con una media de 0 y una desviación estándar de 1.
- simétricas y con un solo punto de elevación
- la media se sitúa al centro, y la desviación estandar expresa su dispersión
- la pendiente es más fuerte cerca del centro, y se suaviza hacia los extremos
- los puntos en los que tiene lugar este cambio de curvatura se hallan a una distancia σ, a ambos lados de la media µ.
Con R es posible generar un conjunto de datos simulados con una distribución normal.
¿Qué estamos haciendo en cada una de las 3 líneas de código? ¿Qué variables se crearon y cómo nos aseguramos de que los datos generados siguieran una distribución normal? Pensemos un poco…
Ahora podemos preguntar qué parte de la curva cae por debajo de un valor particular. Por ejemplo, preguntaremos sobre el valor 0 antes de ejecutar el código. Piense ¿cuál debería ser la respuesta?
pnorm(q = 0)[1] 0.5Tenemos que la probabilidad (en una curva normal estándar) de obtener un valor igual o menor a 0 es de 0.5, es decir, del 50%, pero ¿por qué?
Porque como la distribución normal es simétrica alrededor de cero, la probabilidad de que sea menor o igual a cero es 0.5, es decir, el 50% de la distribución está por debajo de cero y el otro 50% está por encima de cero.
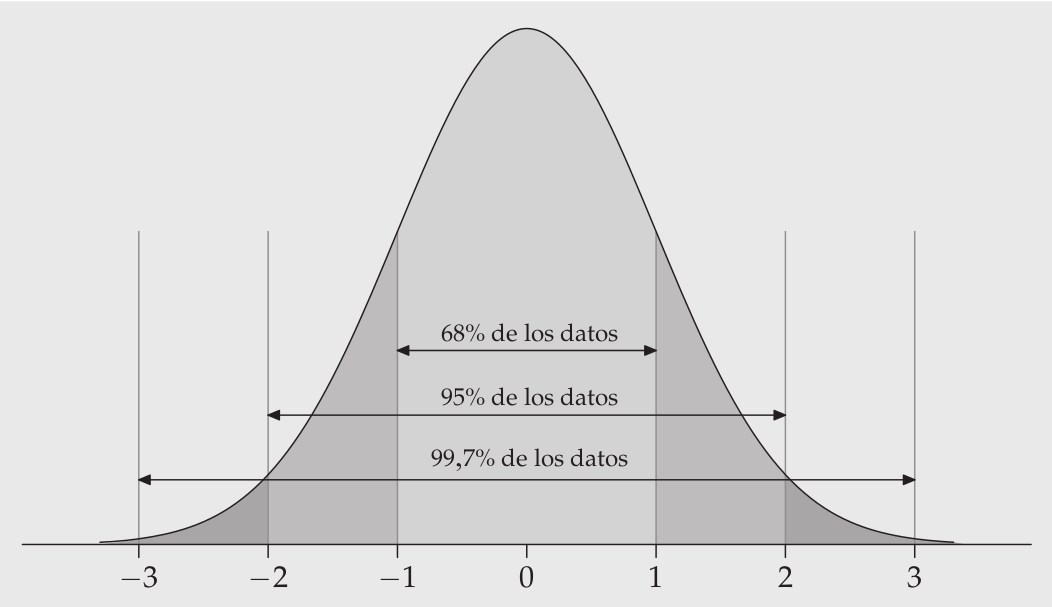
Esto es posible mediante la relación entre las áreas bajo la curva normal y las probabilidades.
Probabilidades asociadas con valores z
Nota
La puntuación Z es una medida que se utiliza para expresar la posición relativa de un valor con respecto a la media en una distribución normal. La puntuación Z mide cuántas desviaciones estándar está un valor por encima o por debajo de la media.
En los ejemplos siguientes, usaremos valores Z de + 1,96 y -1,96 porque sabemos que estos valores aproximados marcan el 2,5% superior e inferior de la distribución normal estándar. Esto corresponde a un alfa típico = 0,05 para una prueba de hipótesis de dos colas (sobre la cual aprenderemos más en las próximas semanas).
pnorm(q = 1.96, lower.tail=TRUE)[1] 0.9750021La respuesta nos dice lo que ya sabemos: el 97,5% de la distribución normal ocurre por debajo del valor z de 1,96.
Podemos agregar una línea al gráfico para mostrar dónde se usaría abline.
El 97,5% de la distribución queda por debajo de esta línea.
plot(x.values, y.values, type="l", lty=1, xlab="Z value", ylab="Probability", main="Normal Distribution") +
abline(v = 1.96)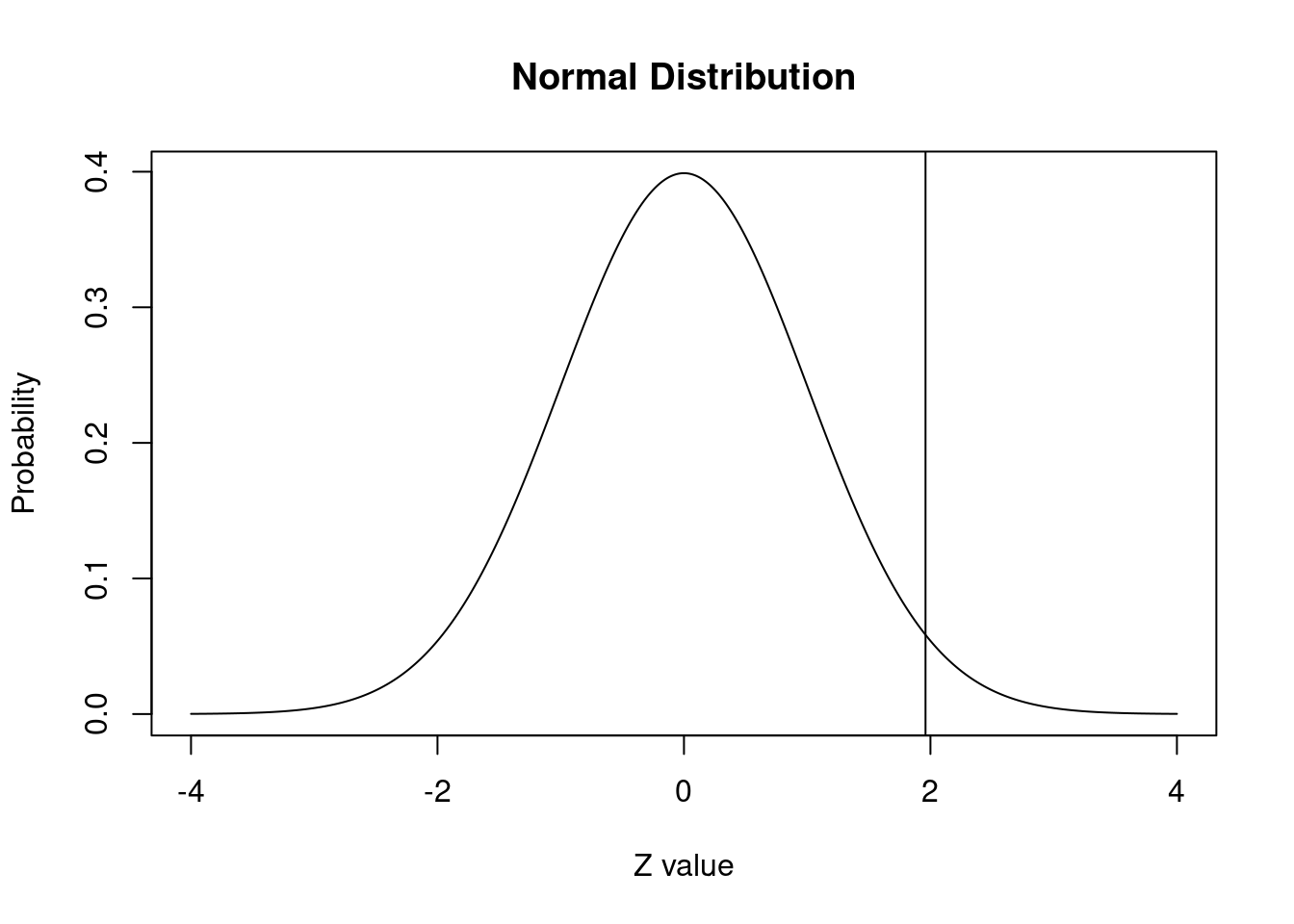
integer(0)¿Y si lo hacemos hacia la cola izquierda o inferior de la distribución?
pnorm(q = -1.96, lower.tail = TRUE)[1] 0.0249979Tenemos que, hacia el extremo inferior de la distribución, el valor z -1,96 marca el 2,5% inferior de la distribución normal estándar.
plot(x.values, y.values, type="l", lty=1, xlab="Z value", ylab="Probability", main="Normal Distribution") +
abline(v = -1.96)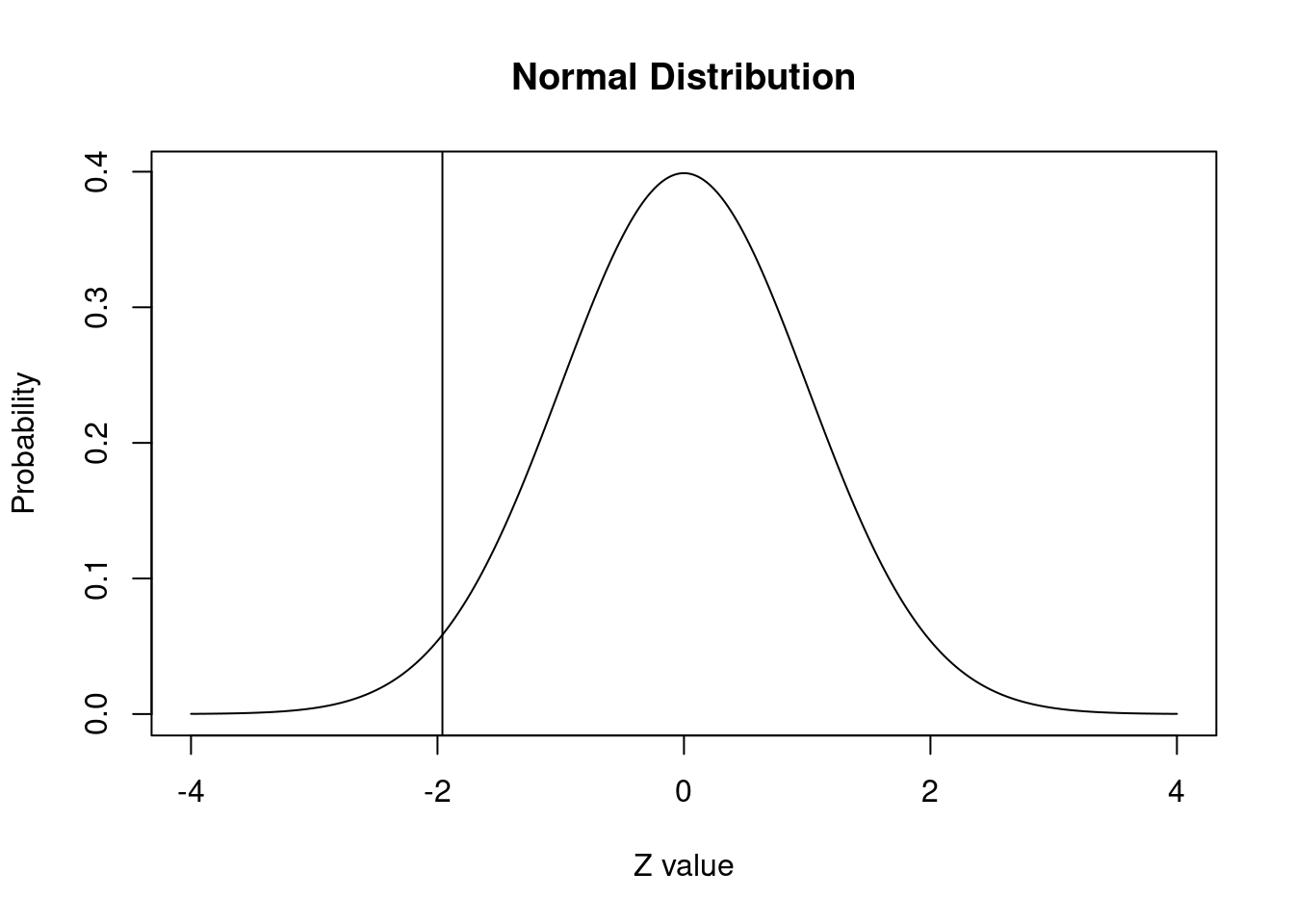
integer(0)Ejercicio 1
Utilice la función abline() para agregar líneas en el puntaje z apropiado para demostrar el clásico 68-95-99.7 de esta curva normal estándar.
plot(x.values, y.values, type="l", lty=1, xlab="Z value", ylab="Probability", main="Normal Distribution") +
abline(v = 1) +
abline(v = -1) +
abline(v = 2) +
abline(v = -2) +
abline(v = 3) +
abline(v = -3)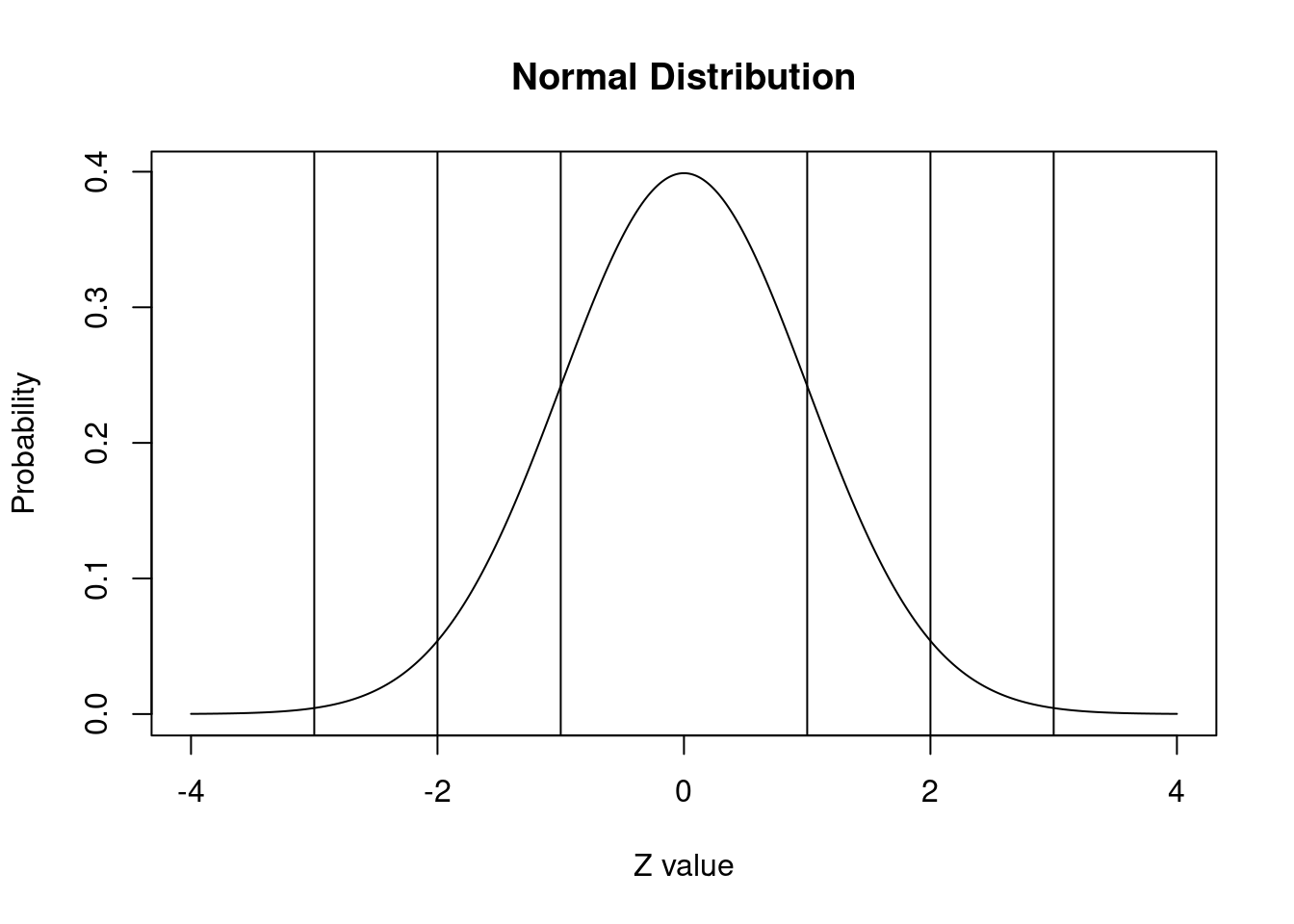
integer(0)Como se discutió en clases, también podemos hacer lo contrario: decidir primero cuánta probabilidad queremos (percentil) y luego calcular qué valores críticos están asociados con esas probabilidades. Esto utiliza la función qnorm. Si queremos saber qué valor z marca la probabilidad p del 2,5% inferior de una distribución normal estándar, usaríamos:
qnorm(p = 0.025)[1] -1.959964Esto nos dice que el valor z de -1,96 marca el 2,5% inferior de la distribución normal estándar. Para determinar el valor z que marca el 2,5% superior de la distribución, escribo:
qnorm(p = 0.975)[1] 1.959964Ejercicio 2
Hasta ahora hemos demostrado todo con una distribución normal estándar. Pero la mayoría de las curvas normales no son normales estándar.
Genere una curva (como hicimos anteriormente para la distribución normal estándar) y trácela con una media de 20 y una desviación estándar de 1,65.
x.values <- seq(10,30, length = 1000)
y.values <- dnorm(x.values, mean = 20, sd = 1.65) # indico media y sd
plot(x.values, y.values, type="l", lty=1, xlab="Z value", ylab="Probability", main="Normal Distribution")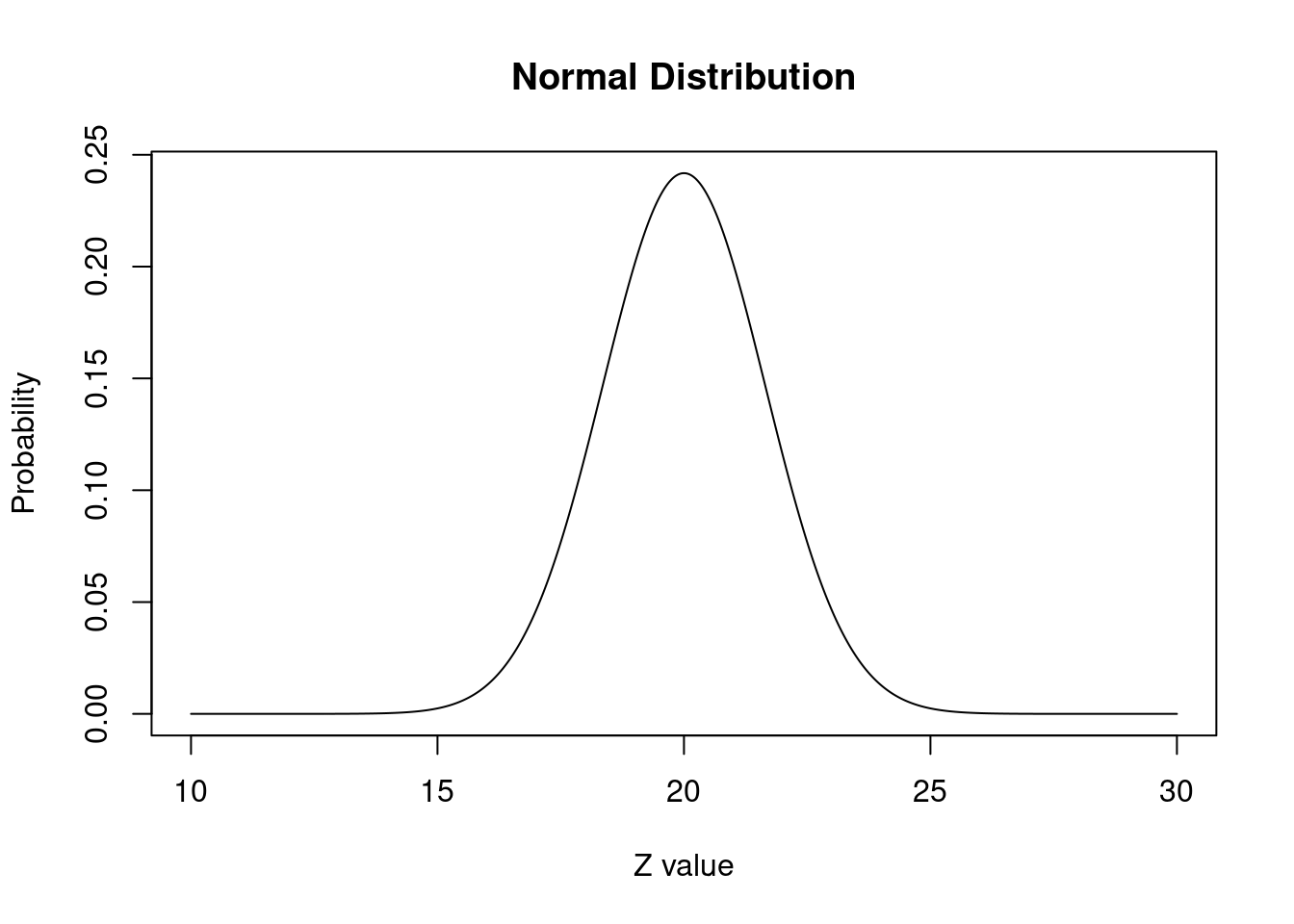
Ahora, identifique el valor en el que el 97,5% de la distribución cae por debajo de este valor. Esto lo hicimos antes con qnorm.
qnorm(p = .975, mean = 20, sd = 1.65)[1] 23.23394Tenemos que el 97,5% de los valores estarán por debajo de 23,2.
Ejercicio de aplicación
Ahora que hemos generado distribuciones normales, echemos un vistazo a algunos datos y compárelos con la distribución normal. Utilizaremos un conjunto de datos desde internet, con mediciones de 247 hombres y 260 mujeres, la mayoría de los cuales eran considerados adultos jóvenes sanos.P uede encontrar una clave para los nombres de las variables aquí, pero nos centraremos en solo tres columnas: peso en kg (wgt), altura en cm (hgt) y sexo (1 = hombre; 0 = mujer).
load(url("http://www.openintro.org/stat/data/bdims.RData"))Separemos estos datos en dos conjuntos, uno de hombres y otro de mujeres con la función subset
mdims <- subset(bdims, sex == 1)
fdims <- subset(bdims, sex == 0)Ejercicio 1
Haz un histograma de la altura de los hombres y un histograma de la altura de las mujeres. ¿Cómo compararía los diversos aspectos de las dos distribuciones?
hist(mdims$hgt, xlim = c(150,200))
hist(fdims$hgt, xlim = c(140,190))
Ejercicio 2
scale es una función en R y se puede aplicar a cualquier vector numérico (lista de números en R). Genere los dos histogramas siguientes, esta vez graficando scale() de las estaturas y determine cómo la versión escalada de las alturas corresponde a las alturas originales. ¿Qué calcula la escala para cada punto?
hist(scale(mdims$hgt))
hist(scale(fdims$hgt))
Ejercicio 3
Nos gustaría comparar la distribución de estaturas en este conjunto de datos con la distribución normal. Para cada uno de los histogramas de alturas (sin escalar), trace una curva normal en la parte superior del histograma.
Calcule la media y la desviación estándar para las alturas femeninas y guárdelas como variables,
fhgtmeanyfhgtsd, respectivamente.Determine la lista de valores de x (el rango del eje X) y guarde este vector. Puede hacer fácilmente una lista de números usando la función
seq()como lo hemos hecho antes, o teniendo el límite inferior:límite superior. Por ejemplo, para generar un vector (lista de números) del 1 al 10 y guardarlo como one_ten, usaría one_ten <- 1:10.Como arriba, use
dnorm()para tomar la lista de valores de x y encontrar el valor de y correspondiente si fuera una distribución normal perfecta. Guarde este vector como la variable y.Vuelva a trazar su histograma y luego, en la siguiente línea, use
lines(x = x, y = y, col = "blue")para dibujar una distribución normal encima.
fhgtmean <- mean(fdims$hgt)
fhgtsd <- sd(fdims$hgt)
hist(fdims$hgt, probability = TRUE, ylim = c(0, .07))
x <- 140:190
y <- dnorm(x = x, mean = fhgtmean, sd = fhgtsd)
lines(x = x, y = y, col = "blue")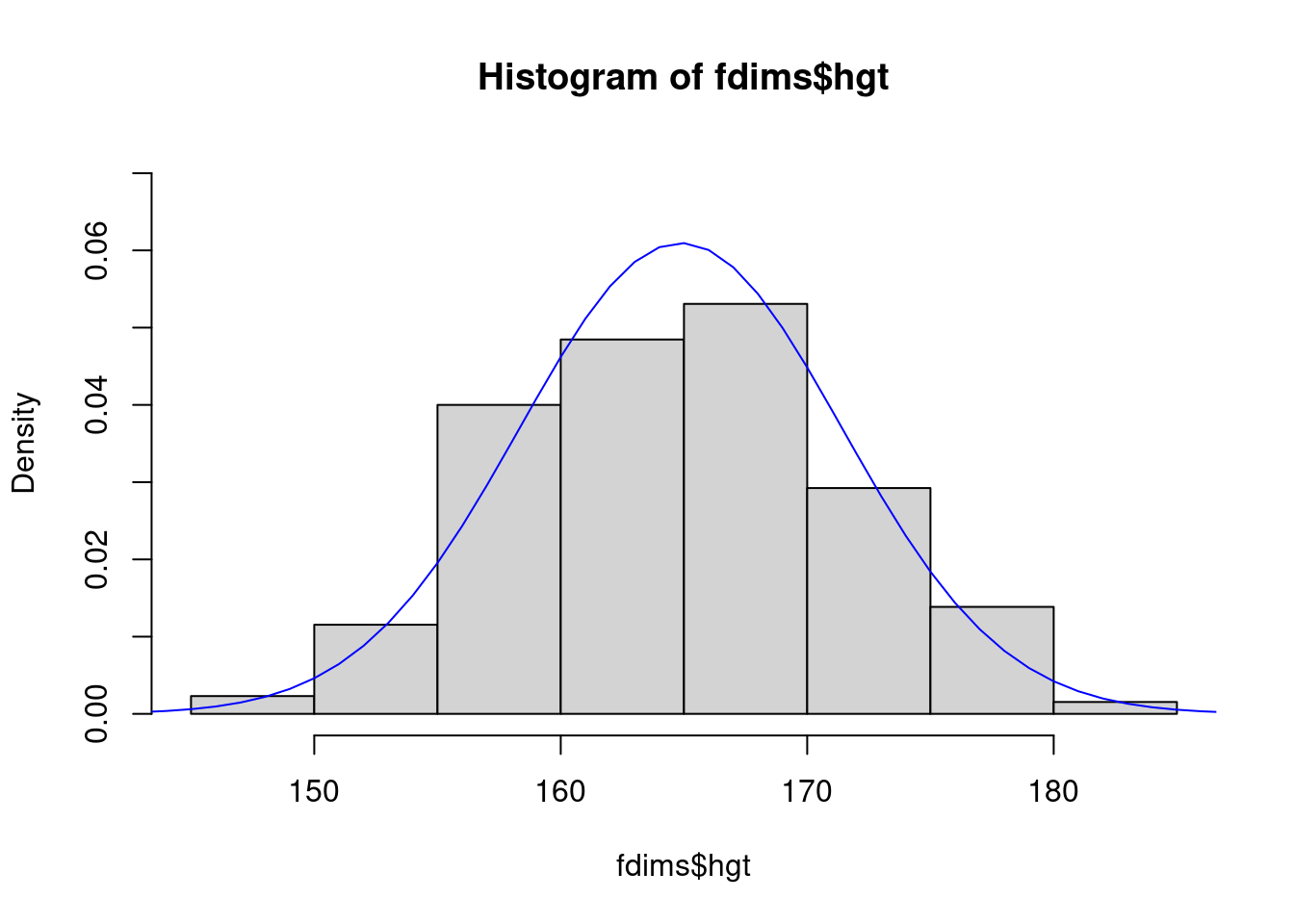
Según este gráfico, ¿parece que los datos siguen una distribución casi normal? Haz lo mismo con las estaturas masculinas.
Respuesta: En general, sí, consideraría que estos valores siguen una distribución casi normal ya que el histograma se ajusta bastante bien a la curva.
Observe que la forma del histograma es una forma de determinar si los datos parecen estar distribuidos casi normalmente, pero puede resultar frustrante decidir qué tan cerca está el histograma de la curva. Un enfoque alternativo implica construir una gráfica de probabilidad normal, también llamada gráfica Q-Q por “quantil-quantil”. Ejecute ambas líneas juntas.
qqnorm(fdims$hgt)
qqline(fdims$hgt)
Un QQ plot nos muestra en el eje x los cuantiles teóricos de la distribución en términos de desviaciones estandar, y en el eje y los valores de la variable. La distribución de los puntos en una línea recta es una indicación de que los datos se distribuyen normalmente.
Veamos otro ejemplo de otra variable de la base de datos:
hist(fdims$che.de)
qqnorm(fdims$che.de)
qqline(fdims$che.de)
Una vez que decidimos que una variable se distribuyte de forma normal, podemos responder todo tipo de preguntas sobre esa variable relacionadas con la probabilidad. Tomemos, por ejemplo, la pregunta: “¿Cuál es la probabilidad de que una mujer adulta joven elegida al azar mida más 182 cm?”
Si suponemos que las alturas de las mujeres se distribuyen normalmente (una aproximación muy cercana también está bien), podemos encontrar esta probabilidad calculando una puntuación Z y consultando una tabla Z (también llamada tabla de probabilidad normal).
En R, esto se hace en un solo paso con la función pnorm (como hicimos anteriormente para la distribución normal estándar).
pnorm(q = 182, mean = fhgtmean, sd = fhgtsd)[1] 0.9955656Obtenemos la proporción de mujeres que está bajo esa estatura, es decir 99,6%. Si queremos saber la proporción de mujeres que está sobre esa estatura:
1 - pnorm(q = 182, mean = fhgtmean, sd = fhgtsd)[1] 0.004434387En este caso, el 0,4% de las mujeres se encontraría sobre esa estatura.
Podemos también hacer la operación inversa, es decir, a qué valor (estatura) corresponde un porcentaje o probabilidad basada en una distribución normal. Para ello utilizamos la función qnorm. Por ejemplo, para la probabilidad que calculamos más arriba para una altura de 182cm en las mujeres:
qnorm(.9955656, fhgtmean, fhgtsd)[1] 182Reporte de progreso
Completar el reporte de progreso correspondiente a esta práctica aquí. El plazo para contestarlo es hasta el día viernes de la semana en la que se publica la práctica correspondiente.