Inferencia 3: Pruebas de hipótesis

Completar hasta as 11:59 PM del martes, 17 de octubre de 2023

Objetivo de la práctica

El objetivo de esta guía práctica es continuar profundizando en la inferencia estadística, en particular en contráste de hipótesis de diferencia de medias. Este tema se desarrolló en la sesión 7.

Test de hipótesis para diferencia de medias

Primero, carguemos las librerías necesarias:

library(pacman)
pacman::p_load(tidyverse,  # colección de paquetes para manipulación de datos
               car,        # para recodificar
               psych,      # para analizar datos
               sjmisc,     # para analizar datos
              # srvyr,      # para estimación de IC y ponderadores
              # Publish,    # para IC
               kableExtra) # para presentación de tablas

options(scipen = 999) # para desactivar notacion cientifica
rm(list = ls()) # para limpiar el entorno de trabajo

Vamos a testear la siguiente hipótesis:

  • \(H_a\): existen diferencias de edad entre hombres y mujeres

Y su correspondiente hipótesis nula:

  • \(H_0\): no existen diferencias de edad entre hombres y mujeres

Generación de datos (muestra_3) y descriptivos:

muestra_3 <- data.frame(edad=c(33,35,23,32,24,25,29,31,32,31),
                        sexo=c(1,1,2,1,2,2,2,1,1,1))

mean(muestra_3$edad)
[1] 29.5
muestra_3$sexo <- as.factor(muestra_3$sexo)

muestra_3 %>% 
  group_by(sexo) %>% 
  summarise(media=mean(edad)) 
# A tibble: 2 × 2
  sexo  media
  <fct> <dbl>
1 1      32.3
2 2      25.2

Gráfico descriptivo:

muestra_3 %>% 
  group_by(sexo) %>% 
  summarise(media=mean(edad)) %>% 
  ggplot(aes(x=sexo, y=media)) +
  geom_point() +
  ylim(25,35) +
  labs(title = "Medias de edad para hombres y mujeres, muestra 3",
                   x = "Sexo",
                   y = "Media edad")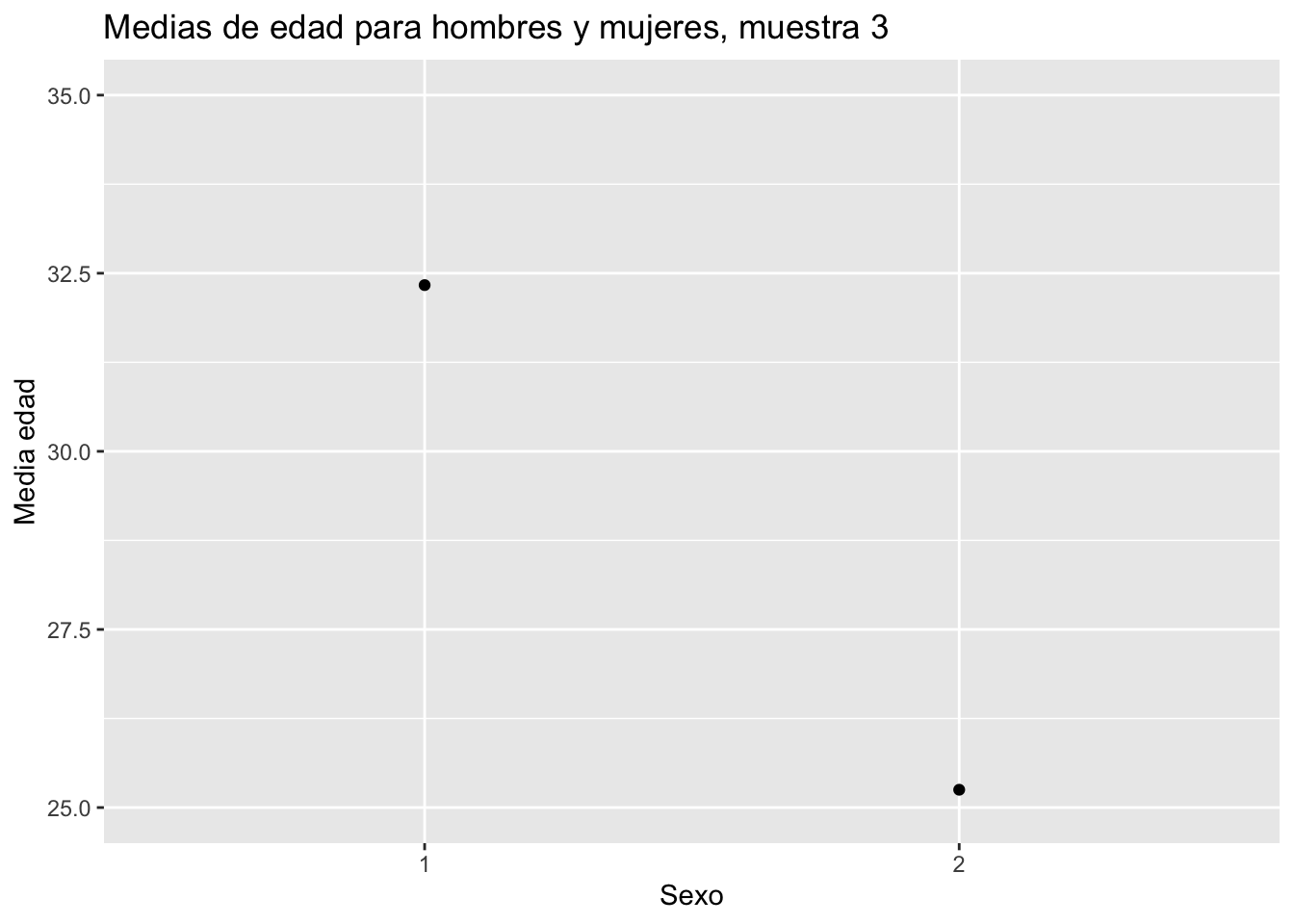

Prueba t de diferencia de medias:

t.test(edad ~ sexo,data=muestra_3)

    Welch Two Sample t-test

data:  edad by sexo
t = 4.8799, df = 4.33, p-value = 0.006658
alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
95 percent confidence interval:
  3.171534 10.995133
sample estimates:
mean in group 1 mean in group 2 
       32.33333        25.25000

Lo principal en este output es el valor p, que es la probabilidad de error de rechazar la hipótesis nula. En este caso, \(p = 0.006658\), que es menor a un nivel de confianza convencional como \(\alpha = 0.05\), incluso es menor que un nivel más exigente como el \(\alpha = 0.01\). Por lo tanto, rechazamos la hipótesis nula de igualdad de medias con un 99% de confianza, hay suficiente evidencia estadística para sostener que el promedio de edad de hombres y mujeres es diferente.

Cálculo paso a paso de estadístico t

En esta última sección se realizará el cálculo paso a paso del estadístico \(t\) del ejemplo anterior para demostrar cómo se origina la información que aparece en el output de R.

Recordemos la fórmula de t:

\(t=\frac{(\bar{x}_1-\bar{x}_2)}{\sqrt{\frac{s_1²}{\sqrt{n_1}}+\frac{s_2²}{\sqrt{n_2}} }}\)

Donde en la parte superior se encuentra la diferencia de medias entre dos grupos, y en la inferior el error estándar de t.

Pasos:

  1. Se calcula la diferencia de medias
  2. Se calcula el error estándar de la diferencia de medias
  3. Cálculo del valor t
  4. Se fija un \(\alpha\) (usualmente 0.05) para rechazar \(H_0\), y se busca el valor crítico asociado a este \(\alpha\) (en una tabla de valores t, o en R)
  5. Si nuestro t es superior al valor crítico, se rechaza \(H_0\)

Paso 1: Calculamos la diferencia de medias \((\bar{x}_1-\bar{x}_2)\)

muestra_3 %>%
   dplyr::group_by(sexo=sjlabelled::as_label(sexo)) %>% # se agrupan por la variable categórica y se usan sus etiquetas con as_label
  dplyr::summarise(Obs.=n(),Promedio=mean(edad, na.rm=TRUE),SD=sd(edad, na.rm=TRUE)) %>% # se agregan las operaciones a presentar en la tabla
  kable(format = "markdown")
sexo Obs. Promedio SD
1 6 32.33333 1.505545
2 4 25.25000 2.629956 
dif_medias <- 32.333 - 25.250
dif_medias
[1] 7.083

Paso 2: Calculamos el error estándar de la diferencia de medias: \(\sqrt{\frac{s_1²}{\sqrt{n_1}}+\frac{s_2²}{\sqrt{n_2}}}\)

muestra_3h <- muestra_3 %>% filter(sexo==1)
muestra_3m <- muestra_3 %>% filter(sexo==2)
  
s_h <- sd(muestra_3h$edad)
n_h <- length(muestra_3h$edad)
s_m <- sd(muestra_3m$edad)
n_m <- length(muestra_3m$edad)

ee <- sqrt((s_h^2)/n_h + (s_m^2)/n_m)
ee
[1] 1.451532

Paso 3: Cálculo del valor t

te <- dif_medias/ee
te
[1] 4.879673

Paso 4: Fijamos un \(\alpha\) y se busca el valor crítico de t asociado al \(\alpha\). En este caso utilizaremos el valor usual de \(\alpha = 0.05\).

tt <- qt(0.05/2,df=9,lower.tail = F)
tt
[1] 2.262157

Paso 5: test de hipótesis

Según la distribución t, el valor crítico para poder rechazar \(H_0\) con un 95% de confianza es 2.26. El t calculado con información de la muestra (o t empírico) es 4.87. Este valor es superior al t crítico, por lo tanto se rechaza \(H_0\) con un 95% de confianza, o una probabilidad de error p<0.05.

Reporte de progreso

Completar el reporte de progreso correspondiente a esta práctica aquí. El plazo para contestarlo es hasta el día martes de la semana siguiente a la que se publica la guía práctica.

Video de práctica

Foro