Inferencia 4: Pruebas de hipótesis II

Completar hasta as 11:59 PM del viernes, 27 de octubre de 2023

Objetivo de la práctica

El objetivo de esta guía práctica es profundizar en la inferencia estadóstica, particularmente en el contraste de hipótesis de diferencias entre dos grupos.

En detalle, aprenderemos:

Aplicar pruebas de hipótesis direccionales.
Aplicar inferencia estadística a proporciones.
Emplear la correlación en contexto de inferencia.

Recursos de la práctica

En esta práctica trabajaremos con un subconjunto de datos previamente procesados de la Encuesta de Caracterización Socioeconómica (CASEN) del año 2022, elaborada por el Ministerio de Desarrollo Social y Familia. Para este ejercicio, obtendremos directamente esta base desde internet. No obstante, también tienes la opción de acceder a la misma información a través del siguiente enlace: CASEN 20222. Desde allí, podrás descargar el archivo que contiene el subconjunto procesado de la base de datos CASEN 2022.

Cinco pasos para la inferencia estadística

En inferencia, las pruebas de hipótesis nos ayudan a determinar si el resultado que obtenemos en nuestra muestra es un efecto real/extensible a la población o un error de muestreo. Aquí recomendamos una lista de cinco pasos lógicos para enfrentarnos a la inferencia estadística:

Paso	Detalle
1	Formula \(H_0\) y \(H_A\) y estipula la dirección de la prueba
2	Calcula el error estándar (SE)
3	Calcula el valor estimado de la prueba (ej: Z o t)
4	Especifica el valor crítico de la prueba
5	Contrasta el valor estimado con el valor crítico e intrepreta los resultados

Además de estos 5 pasos también existe la posibilidad de calcular un intervalo de confianza, que acompañe la precisión de nuestra estimación.

Preparación datos

Comencemos por preparar nuestros datos. Iniciamos cargando las librerías necesarias.

pacman::p_load(tidyverse, # Manipulacion datos
               sjPlot, #tablas
               confintr, # IC
               gginference, # Visualizacion 
               rempsyc, # Reporte
               broom) # Varios

options(scipen = 999) # para desactivar notacion cientifica
rm(list = ls()) # para limpiar el entorno de trabajo

Cargamos los datos directamente desde internet.

load(url("https://github.com/cursos-metodos-facso/datos-ejemplos/raw/main/proc_casen.RData")) #Cargar base de datos

A continuación, exploramos la base de datos proc_casen.

names(proc_casen) # Nombre de columnas

 [1] "id_vivienda"      "folio"            "id_persona"       "hogar"           
 [5] "nucleo"           "varunit"          "varstrat"         "expr"            
 [9] "edad"             "sexo"             "educ"             "activ"           
[13] "y1"               "ytrabajocor"      "pobreza_multi_5d" "o15"             
[17] "fdt"              "ocupado"          "desocupado"       "inact"           
[21] "hijo"             "n_educ"           "universitaria"    "tipo_ocup"

dim(proc_casen) # Dimensiones

[1] 202111     24

Contamos con 24 variables (columnas) y 202.111 observaciones (filas).

Recordemos…

En estadística, la formulación de hipótesis que implica dos variables (o la comparación de grupos) busca determinar si existen diferencias en una variable entre grupos y, de ser el caso, evaluar si esta diferencia es estadísticamente significativa.

Hasta ahora, hemos aprendido a contrastar hipótesis sobre diferencias entre grupos. A esto también se le llama hipótesis de dos colas.

Prueba de dos colas

Contrastamos la hipótesis nula (o de trabajo) de no diferencias entre grupos: \[ H_{0}: \mu_{1} - \mu_{2} = 0 \] En relación a una hipótesis alternativa sobre diferencias entre grupos: \[ H_{A}: \mu_{1} - \mu_{2} \neq 0 \]

Veamos un ejemplo con nuestros datos. Evaluemos si el promedio de ingresos del trabajo de las mujeres es distinto al de los hombres en Chile en el 2022.

Apliquemos nuestros cinco pasos para inferencia.

Formulamos nuestras hipótesis y dirección de la prueba:

\(H_{0}\): \(\mu_{hombres}\) \(-\) \(\mu_{mujeres}\) \(=\) \(0\)
\(H_{A}\): \(\mu_{hombres}\) \(-\) \(\mu_{mujeres}\) \(\neq\) \(0\)

Calcula el error estándar (SE) para diferencia de medias:

ocupados <- proc_casen %>%
  filter(ocupado == 1) %>% 
  na.omit() #  subset de datos solo con personas ocupadas

datos_t <- ocupados %>% 
  group_by(sexo) %>% 
  summarise(media = mean(ytrabajocor, na.rm = T),
            ds = sd(ytrabajocor, na.rm = T),
            n = n())

datos_t

# A tibble: 2 × 4
   sexo   media      ds     n
  <dbl>   <dbl>   <dbl> <int>
1     1 817688. 837711. 32019
2     2 674428. 638044. 26313

Obtenemos la diferencia de medias (\(\bar{x_1}\) - \(\bar{x_2}\))

dif_medias <- 817688.2 - 674428.3
dif_medias

[1] 143259.9

Ahora, calculamos el error estándar.

s_h <- 837710.9 
s_m <- 638044.1

n_h <- 32019 
n_m <- 26313    

se_dif <- sqrt((s_h^2)/n_h + (s_m^2)/n_m)
se_dif

[1] 6114.607

Calcula el valor estimado de la prueba (t para diferencia de medias):

t_stat <- dif_medias/se_dif
t_stat

[1] 23.42912

Especifica el valor crítico:

df <- n_h + n_m - 2 # definimos grados de libertad

t_critico <- qt(p = 0.05/2, df, lower.tail = FALSE)
t_critico

[1] 1.960005

Contrasta el valor estimado con el crítico e interpreta los resultados:

t_stat > t_critico

[1] TRUE

Comparamos el valor estimado con el valor crítico para dos colas. Por tanto, nuestro valor estimado queda dentro de la zona de rechazo de \(H_0\). En consecuencia, podemos decir que:

La prueba T que evalúa la diferencia de medias entre el ingreso del trabajo según sexo sugiere que el efecto es positivo y estadísticamente signficativo (diferencia = 143.260, t(58004.33) = 23.43, p < .001). Por tanto, rechazamos la \(H_{0}\) sobre igualdad de medias con un 95% de confianza, existiendo evidencia a favor de nuestra \(H_{A}\) ya que hay diferencias salariales significativas entre hombres y mujeres.

Y el cálculo directo en R:


t_results <- t.test(ocupados$ytrabajocor ~ ocupados$sexo, 
       alternative = "two.sided")

stats.table <- tidy(t_results, conf_int = T)
nice_table(stats.table, broom = "t.test")

Method	Alternative	Mean 1	Mean 2	M1 - M2	t	df	p	95% CI
Welch Two Sample t-test	two.sided	817,688.24	674,428.29	143,259.95	23.43	58,004.33	< .001***	[131275.29, 155244.61]

Visualicemos la distribución de esta prueba y su zona de rechazo.

ggttest(t_results)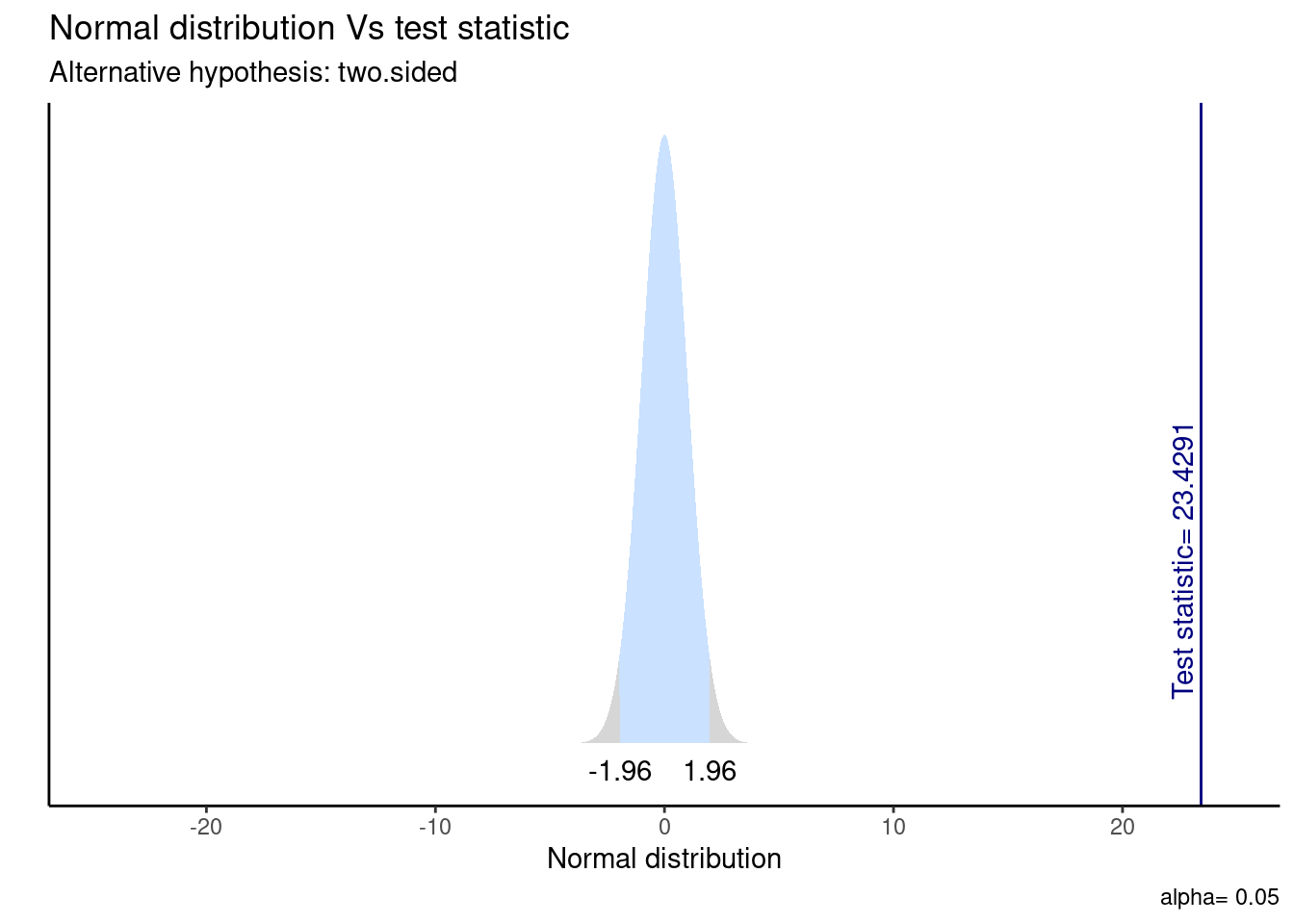

Además, podemos calcular un intervalo de confianza que acompaña nuestra estimación. En este caso, vemos que el IC para la diferencia de medias oscila entre [131.275 - 155.245] y no contiene el cero, por lo que podemos rechazar la hipótesis nula.

Pruebas de hipótesis direccionales para la media

Sin embargo, también podemos plantear hipótesis respecto a que el valor de cierto parámetro para un grupo puede ser mayor o menor al de otro grupo. A esto se le conoce como hipótesis de una cola.

Prueba de una cola

\[ H_{0}: \mu_{0} ≥ \mu_{1} ; \mu_{0} ≤ \mu_{1}\]

\[ H_{A}: \mu_{0} > \mu_{1} \]

\[ H_{A}: \mu_{0} < \mu_{1} \]

Tomando como ejemplo el trabajo de la ganadora del Premio Nobel de Economía 2023 Claudia Goldin, comprobemos si los ingresos de las mujeres trabajadoras que no tienen hijos es mayor al ingreso de las mujeres trabajadoras que sí tienen hijos. Por tanto, usaremos prueba \(t\) para diferencia de medias.

Apliquemos nuestros 5 pasos.

Formulamos nuestras hipótesis y dirección de la prueba:

En donde 0 = sin hijos y 1 = con hijos;

\(H_{0}\): \(\mu_{0}\) \(≤\) \(\mu_{1}\)
\(H_{A}\): \(\mu_{0}\) \(>\) \(\mu_{1}\)

Calcula el error estándar (SE) para diferencia de medias:

goldin_data <- proc_casen %>% 
  filter(ocupado == 1 & sexo == 2) %>% 
  na.omit()# creamos subset con solo mujeres ocupadas

datos_t <- goldin_data %>% 
  group_by(hijo) %>% 
  summarise(media = mean(ytrabajocor, na.rm = T),
            ds = sd(ytrabajocor, na.rm = T),
            n = n()) 

datos_t

# A tibble: 2 × 4
   hijo   media      ds     n
  <dbl>   <dbl>   <dbl> <int>
1     0 729850. 659401.  6807
2     1 655088. 629291. 19506

En este caso, obtenemos la diferencia de medias (\(\bar{x}_0 - \bar{x}_1\) ).

dif_medias <- 729850.1 - 655087.8
dif_medias

[1] 74762.3

Y luego su error estándar.

s_0 <- 659400.5 
s_1 <- 629290.5

n_0 <- 6807 
n_1 <- 19506    

se_dif <- sqrt((s_0^2)/n_0 + (s_1^2)/n_1)
se_dif

[1] 9174.886

Calcula el valor estimado de la prueba (t para diferencia de medias):

t_stat <- dif_medias / se_dif

t_stat

[1] 8.148581

Especifica el valor crítico:

df <- n_0 + n_1 - 2 # definimos grados de libertad

t_critico <- qt(p = 0.05, df, lower.tail = FALSE)

t_critico

[1] 1.644912

Contrasta el valor estimado con el crítico e interpreta los resultados:

t_stat > t_critico

[1] TRUE

La prueba T que evalúa la diferencia de medias entre el ingreso del trabajo y tener hijos en las mujeres ocupadas sugiere que el efecto es positivo y estadísticamente signficativo (diferencia = 74.762, t(11417.34) = 8.15, p < .05). Por tanto, con un 95% de confianza, rechazamos la \(H_{0}\) ya que existe evidencia a favor de nuestra \(H_{A}\) respecto a que el ingreso de las mujeres sin hijos es mayor al ingreso de las mujeres con hijos.

Y el cálculo en R.

t_results_goldin <- t.test(goldin_data$ytrabajocor ~ goldin_data$hijo, 
                           alternative = "greater") # indicamos la direccion de la prueba

stats.table <- tidy(t_results_goldin, conf.int = T)
nice_table(stats.table, broom = "t.test")

Method	Alternative	Mean 1	Mean 2	M1 - M2	t	df	p	95% CI
Welch Two Sample t-test	greater	729,850.11	655,087.76	74,762.34	8.15	11,417.34	< .001***	[59669.77, Inf]

Visualicemos la distribución de esta prueba y su zona de rechazo.

ggttest(t_results_goldin)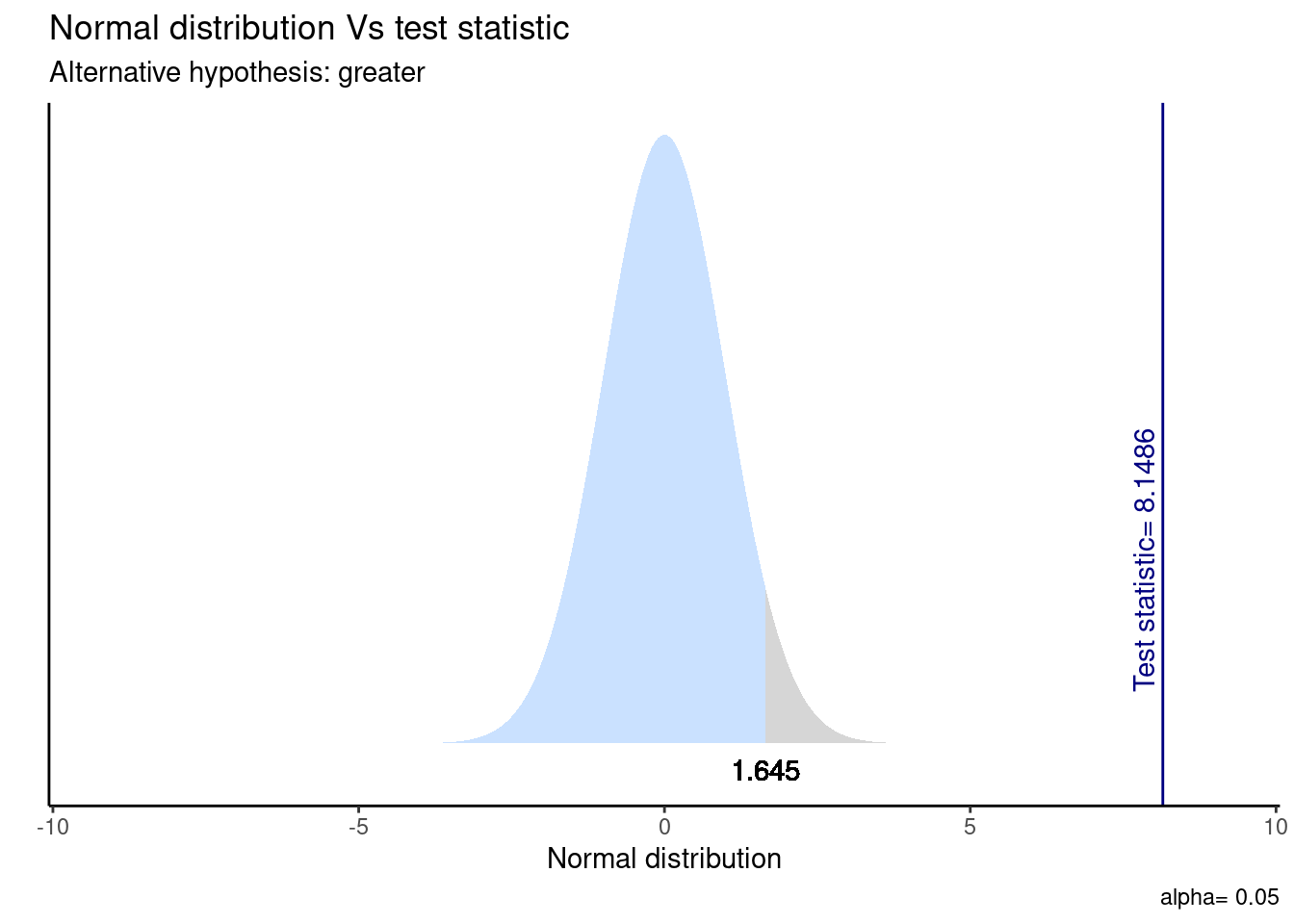

En este caso, el IC del 95% es (59.670, Inf), donde “Inf” representa infinito. Esto significa que podemos estar 95% seguros de que la diferencia real entre las medias está por encima de 59.670. En otras palabras, con alta confianza, podemos afirmar que la media del “grupo 0” es significativamente mayor que la del “grupo 1”.

Inferencia para proporciones

Cuando queremos realizar inferencia para variables categóricas, generlamente utilizamos pruebas que comparan proporciones de una variable de interés entre grupos.

El test de proporciones es una prueba estadística utilizada para determinar si hay una diferencia significativa entre dos proporciones (tasas) en dos grupos. Se basa en datos categóricos, en donde se cuentan los eventos “exitosos” o “positivos” en cada grupo de comparación, por sobre el total de eventos.

Evaluamos si existen diferencias entre hombres y mujeres en la proporción de encontrarse en situación de pobreza multidimensional.

pobreza <- proc_casen[1:300,] # creamos un subsample solo como ejemplo

sjPlot::sjt.xtab(pobreza$pobreza_multi_5d, pobreza$sexo, show.col.prc = T)

situación de pobreza multidimensional con entorno y redes (5 dimensiones)	Sexo		Total
	1. Hombre	2. Mujer	Total
No pobreza	91 67.9 %	115 71 %	206 69.6 %
Pobreza	43 32.1 %	47 29 %	90 30.4 %
Total	134 100 %	162 100 %	296 100 %
χ²=0.199 · df=1 · φ=0.033 · p=0.656

Formulemos nuestras hipótesis:

\(H_0\): \(p_{hombres}\) \(=\) \(p_{mujeres}\)
\(H_A\): \(p_{hombres}\) \(\neq\) \(p_{mujeres}\)

Ahora, creemos un objeto llamado xtab que contendrá la frecuencia de casos exitosos (“pobreza”) sobre el total de casos para cada grupo.

xtab <- as.table(rbind(c(43, 47),c(91, 115)))

dimnames(xtab) <- list(
  pobreza = c("si", "no"),
  sexo = c("hombre", "mujer")
)

Luego, aplicamos la función prop.test() para evaluar nuestra hipótesis.

prop_results <- prop.test(xtab, alternative = "two.sided")

stats.table <- tidy(prop_results, conf.int = T)
nice_table(stats.table, broom = "prop.test")

estimate1	estimate2	t	p	df	Method	Alternative	95% CI
0.48	0.44	0.20	.656	1	2-sample test for equality of proportions with continuity correction	two.sided	[-0.10, 0.17]

¿Y cómo reportamos esto?:

Esta prueba que evalúa la diferencia de proporciones entre encontrarse en situación de pobreza según sexo sugiere que el efecto es positivo y estadísticamente no significativo (\(X^2\)= 0.19887, p = 0.6556). Por tanto, no se rechaza la \(H_{0}\) sobre igualdad de proporciones ya que no existe suficiente evidencia para concluir que las proporciones en los dos grupos son significativamente diferentes.

Además de lo anterior, vemos que en este caso el IC de diferencia de proporciones sí contiene el cero, por lo que no podemos rechazar la hipótesis nula.

Inferencia en correlación

En el contexto de la inferencia, la correlación nos permite determinar si existe (o no) una asociación estadísticamente significativa entre dos variables. En ese sentido, la lógica del contraste de hipótesis usando correlación es:

Hipótesis en correlación

Contrastamos la hipótesis nula (o de trabajo) de no asociación entre variables: \[ H_{0}: \rho = 0 \]

En relación a una hipótesis alternativa sobre la existencia una asociación significativa entre variables:

\[ H_{A}: \rho \neq 0 \]

Tomemos por ejemplo la siguiente pregunta de investigación: ¿en qué medida el nivel educacional alcanzado por las personas se relaciona con sus ingresos en Chile en el 2022?

Formulemos nuestra hipótesis:

\(H_{0}\): \(cor(educ,ingreso)\) \(=\) \(0\)
\(H_{A}\): \(cor(educ,ingreso)\) \(\neq\) \(0\)

Obtengamos el coeficiente de correlación \(r\) de Pearson entre el nivel educacional alcanzado y los ingresos de las personas en Chile en 2022. Para esto usaremos solamente observaciones completas (listwise).

cor_results <- cor.test(proc_casen$educ, proc_casen$ytrabajocor, 
         method = "pearson", 
         use = "complete.obs")

stats.table <- tidy(cor_results)
nice_table(stats.table, broom = "cor")

estimate	t	p	df	Method	Alternative	95% CI
0.38	123.36	< .001***	88,290	Pearson's product-moment correlation	two.sided	[0.38, 0.39]

Ya sabemos cómo interpretar una correlación, ahora usemos este resultado para probar nuestra hipótesis:

El coeficiente de correlación de Pearson entre nivel educativo e ingresos es positivo, estadísticamente significativo (r = 0.38, p < .001) y moderado de acuerdo con las recomendaciones de Cohen (1988). Por tanto, con un 95% de confianza se puede rechazar la \(H_{0}\) de no asociación entre variables, existiendo evidencia a favor de la \(H_{A}\) sobre una asociación significativa entre educación e ingresos.

Resumen

Hoy profundizamos en la inferencia estadóstica, particularmente en el contraste de hipótesis de diferencias entre dos grupos.

En detalle, aprendimos a:

Aplicar pruebas de hipótesis direccionales.
Aplicar inferencia estadística a proporciones.
Emplear la correlación en contexto de inferencia.

Reporte de progreso

Completar el reporte de progreso correspondiente a esta práctica aquí. El plazo para contestarlo es hasta el día viernes de la semana en la que se publica la práctica correspondiente.