Matrices de correlación y tamaños de efecto

Completar hasta as 11:59 PM del viernes, 1 de septiembre de 2023

Objetivo de la práctica

El objetivo de esta guía práctica es conocer maneras de reportar coeficientes de correlación y cómo interpretar sus tamaños de efecto en ciencias sociales. Además, nos introduciremos en el tratamiento de valores perdidos y otras medidas de correlación entre variables.

En detalle, aprenderemos:

  1. Cómo reportar y presentar matrices de correlación.
  2. Interpretar el tamaño de efecto de una correlación.
  3. Tratamiento de casos perdidos.
  4. Qué es y cómo calcular la correlación de Spearman.
  5. Qué es el coeficiente de determinación \(R^2\).
Nota

¿Qué era la correlación?

La correlación es una medida de asociación entre variables, que describe el sentido (dirección) y fuerza de la asociación.

En otras palabras, nos permite conocer cómo y cuánto se relaciona la variación de una variable, con la variación de otra variable.

Recursos de la práctica

En esta práctica trabajaremos con un subconjunto de datos previamente procesados del Estudio Longitudinal Social de Chile (ELSOC) del año 2016, elaborado por COES. Para este ejercicio, obtendremos directamente esta base desde internet. No obstante, también tienes la opción de acceder a la misma información a través del siguiente enlace: ELSOC 2016. Desde allí, podrás descargar el archivo que contiene el subconjunto procesado de la base de datos ELSOC 2016.

Preparación datos

Comencemos por preparar nuestros datos. Iniciamos cargando las librerías necesarias.

pacman::p_load(tidyverse, # Manipulacion datos
               sjmisc, # Descriptivos
               sjPlot, # Tablas
               kableExtra, #Tablas
               GGally, # Correlaciones
               corrplot) # Correlaciones

options(scipen = 999) # para desactivar notacion cientifica
rm(list = ls()) # para limpiar el entorno de trabajo

Cargamos los datos directamente desde internet (por esta vez).

load(url("https://multivariada.netlify.app/assignment/data/proc/ELSOC_ess_merit2016.RData")) #Cargar base de datos

A continuación, exploramos la base de datos proc_elsoc.

names(proc_elsoc) # Nombre de columnas
[1] "mesfuerzo" "mtalento"  "ess"       "edcine"    "sexo"      "edad"     
[7] "pmerit"   
dim(proc_elsoc) # Dimensiones
[1] 2927    7

Contamos con 7 variables (columnas) y 2927 observaciones (filas).

Ahora, profundicemos un poco más y observemos algunos estadísticos descriptivos de resumen de nuestra base de datos. Utilizaremos la función descr del paquete sjmisc.

sjmisc::descr(proc_elsoc,
      show = c("label","range", "mean", "sd", "NA.prc", "n")) %>%
      kable(.,"markdown")
var label n NA.prc mean sd range
4 mesfuerzo Recompensa: esfuerzo 2909 0.6149641 2.5727054 1.0466874 4 (1-5)
5 mtalento Recompensa: talento 2907 0.6832935 2.7389061 1.0596182 4 (1-5)
3 ess Estatus Social Subjetivo 2915 0.4099761 4.3300172 1.5666965 10 (0-10)
2 edcine Educación 2925 0.0683293 3.1839316 1.2066058 4 (1-5)
7 sexo Sexo 2927 0.0000000 0.6026648 0.4894300 1 (0-1)
1 edad Edad 2927 0.0000000 46.0908780 15.2867983 70 (18-88)
6 pmerit Meritocracia promedio 2898 0.9907755 2.6538992 0.9694792 4 (1-5)

¡ALTO! Tenemos algunos valores o casos perdidos en ciertas variables. ¿Cómo lidiar con los casos perdidos?

Tratamiento de casos perdidos

Trabajar con datos a menudo implica enfrentar valores perdidos (NA), lo que puede ser un gran desafío. Estos valores indican la ausencia de un valor en una base de datos. Los valores perdidos pueden originarse por diversas razones, como el sesgo de no respuesta en encuestas, errores en la entrada de datos o simplemente la falta de información para ciertas variables.

X1 X2 X3 X4
NA 4 1 Hola
7 1 4 No soy un NA
8 NA 2 NA
9 NA 9 Amo R
3 3 6 NA

La presencia de valores perdidos puede tener un impacto considerable en la precisión y confiabilidad de los análisis estadísticos, lo que a su vez puede conducir a resultados sesgados y conclusiones incorrectas.

Existen varias formas de tratar valores perdidos, que van desde enfoques simples hasta métodos más complejos, como la imputación. En esta ocasión, nos centraremos en las dos estrategias más comunes:

  • trabajar exclusivamente con casos completos (listwise) o
  • retener los casos con valores perdidos, pero excluyéndolos al calcular estadísticas (pairwise).

a) Analísis con casos completos: listwise deletion

Este enfoque es uno de los más conocidos: implica remover completamente las observaciones que tienen valores perdidos en cualquier variable de interés. En otras palabras, si una fila/caso en un conjunto de datos tiene al menos un valor faltante en alguna de las variables que estás considerando, se eliminará por completo.

En R, esto podemos hacerlo con la función na.omit. Para hacer esto, sigamos estos pasos:

  • respaldar la base de datos original en el espacio de trabajo (por si queremos en adelante realizar algún análisis referido a casos perdidos)-
  • contamos el número de casos con el comando dim.
  • contamos cuántos y en dónde tenemos casos perdidos.
  • borramos los casos perdidos con na.omit.
  • contamos nuevamente con dim para asegurarnos que se borraron.
proc_elsoc_original <- proc_elsoc
dim(proc_elsoc)
[1] 2927    7
sum(is.na(proc_elsoc))
[1] 81
colSums(is.na(proc_elsoc))
mesfuerzo  mtalento       ess    edcine      sexo      edad    pmerit 
       18        20        12         2         0         0        29 
proc_elsoc <- na.omit(proc_elsoc)
dim(proc_elsoc)
[1] 2887    7

Ahora nos quedamos con 2887 observaciones sin casos perdidos.

Aunque simple de implementar, con este enfoque podemos perder información importante, especialmente si los valores perdidos no se distribuyen aleatoriamente.

Siempre hay que intentar rescatar la mayor cantidad de casos posibles. Por lo tanto, si un listwise genera más de un 10% de casos perdidos se debe detectar qué variables esta produciendo esta pérdida e intentar recuperar datos. Puedes revisar un ejemplo aquí.

b) Retener pero excluir: pairwise deletion

A diferencia del anterior, este es un enfoque en el que las observaciones se utilizan para el análisis siempre que tengan datos disponibles para las variables específicas que se están analizando. En lugar de eliminar toda una fila si falta un valor, se eliminan solo los valores faltantes en las variables que se están analizando en ese momento.

Para hacer esto en R debemos siempre verificar e indicar en nuestro código si queremos (o no) remover los NA para realizar los análisis.

mean(proc_elsoc_original$pmerit); mean(proc_elsoc$edad); mean(proc_elsoc$ess)
[1] NA
[1] 45.98337
[1] 4.333564
mean(proc_elsoc_original$pmerit, na.rm = TRUE); mean(proc_elsoc$edad, na.rm = TRUE); mean(proc_elsoc$ess, na.rm = TRUE)
[1] 2.653899
[1] 45.98337
[1] 4.333564

Con el primer código no obtuvimos información sustantiva en ciertas variables, pero con el segundo sí al remover los NA solo de dicha variable para un cálculo determinado.

Matrices de correlación

La correlación es una estimación de asociación de dos variables. Sin embargo, en los análisis de bases de datos usualmente se exploran asociaciones entre múltiples pares de variables, lo que genera una matriz de correlación. En una matriz, las variables se presentan en las filas y las columnas, y en las celdas donde se cruzan los pares de variables se muestra su coeficiente de correlación.

En su forma simple en R se aplica la función cor a la base de datos, y la guardamos en un objeto que le damos el nombre M para futuras operaciones:

M <- cor(proc_elsoc_original, use = "complete.obs") 
M
             mesfuerzo    mtalento          ess      edcine        sexo
mesfuerzo  1.000000000  0.69768811 -0.004312135 -0.12167659 -0.04480502
mtalento   0.697688106  1.00000000  0.018447696 -0.10582754 -0.03759340
ess       -0.004312135  0.01844770  1.000000000  0.28959248 -0.03745546
edcine    -0.121676591 -0.10582754  0.289592479  1.00000000 -0.08682644
sexo      -0.044805024 -0.03759340 -0.037455462 -0.08682644  1.00000000
edad       0.096495547  0.07383771 -0.066031873 -0.37660283  0.06121699
pmerit     0.920404032  0.92224547  0.007740598 -0.12341680 -0.04469515
                 edad       pmerit
mesfuerzo  0.09649555  0.920404032
mtalento   0.07383771  0.922245465
ess       -0.06603187  0.007740598
edcine    -0.37660283 -0.123416804
sexo       0.06121699 -0.044695146
edad       1.00000000  0.092369792
pmerit     0.09236979  1.000000000

Este es el reporte simple, pero no muy amigable a la vista. Para una versión más reportable, utilizamos la funcion tab_corr.

sjPlot::tab_corr(proc_elsoc_original, 
                 triangle = "lower")
  Recompensa: esfuerzo Recompensa: talento Estatus Social Subjetivo Educación Sexo Edad Meritocracia promedio
Recompensa: esfuerzo              
Recompensa: talento 0.698***            
Estatus Social Subjetivo -0.004 0.018          
Educación -0.122*** -0.106*** 0.290***        
Sexo -0.045* -0.038* -0.037* -0.087***      
Edad 0.096*** 0.074*** -0.066*** -0.377*** 0.061**    
Meritocracia promedio 0.920*** 0.922*** 0.008 -0.123*** -0.045* 0.092***  
Computed correlation used pearson-method with listwise-deletion.

La distinción entre listwise y pairwise es relevante al momento de estimar matricies de correlación, donde esta decisión debe estar claramente explicitada y fundamentada. En ejemplo de tabla anterior usamos listwise que es el argumento por defecto (y nos lo indica al final de la tabla).

Veamos como hacerlo con pairwise:

sjPlot::tab_corr(proc_elsoc_original, 
                 na.deletion = "pairwise", # espeficicamos tratamiento NA
                 triangle = "lower")
  Recompensa: esfuerzo Recompensa: talento Estatus Social Subjetivo Educación Sexo Edad Meritocracia promedio
Recompensa: esfuerzo              
Recompensa: talento 0.696***            
Estatus Social Subjetivo -0.006 0.016          
Educación -0.124*** -0.109*** 0.287***        
Sexo -0.044* -0.036 -0.035 -0.090***      
Edad 0.099*** 0.075*** -0.068*** -0.379*** 0.062***    
Meritocracia promedio 0.920*** 0.922*** 0.008 -0.125*** -0.043* 0.092***  
Computed correlation used pearson-method with pairwise-deletion.

Con esta mejor visualización, algunas observaciones sobre la matriz de correlaciones:

  • En esta matriz las variables están representadas en las filas y en las columnas.
  • Cada coeficiente expresa la correlación de una variable con otra. Por ejemplo, la correlación entre la variable de mesfuerzo y mtalento es 0.69.
  • La información de cada coeficiente se repite sobre y bajo la diagonal, ya que es el mismo par de variables pero en el orden alterno. Por convención en general se omiten las correlaciones redundantes sobre la diagonal, por eso aparece en blanco.
  • En la diagonal corresponde que todos los coeficientes sean 1, ya que la correlación de una variable consigo misma es perfectamente positiva.

Otra manera de presentar matrices de correlación es mediante gráficos. Veamos un ejemplo con la función corrplot.mixed de la librería corrplot sobre nuestra matriz M ya creada.

corrplot.mixed(M)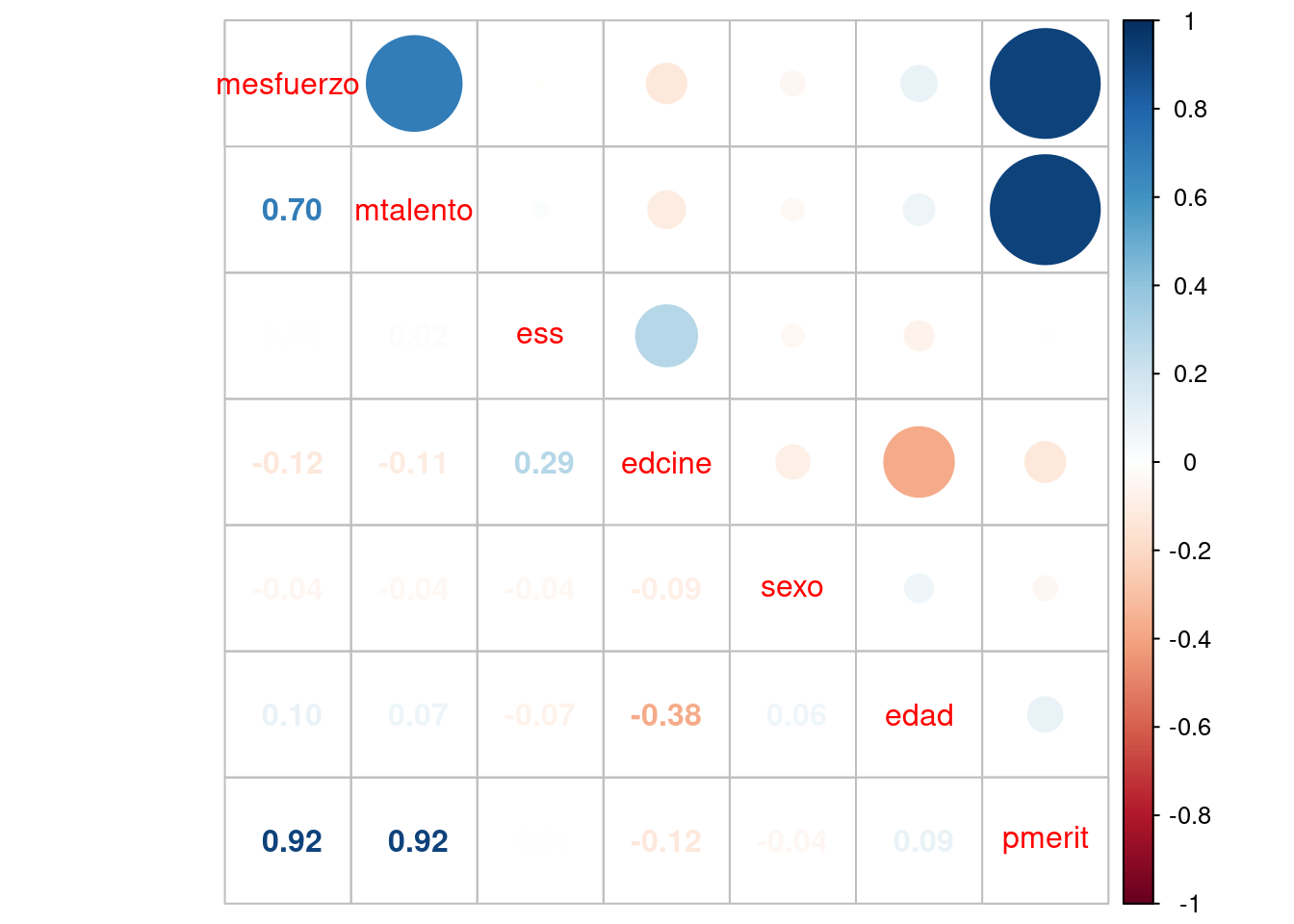

Este gráfico/matriz representa el grado de asociación entre variables mediante el tamaño de los círculos e intensidad de colores, y el signo de la asociación se representa con una gradiente de colores que va del azul (positivo) al rojo (negativo).

Otra manera de graficar la matriz es con la función ggpairs del paquete GGally, que nos entrega no solo el valor del coeficiente y su significancia (***), si no que también un scatter del cruce entre variables.

ggpairs(proc_elsoc)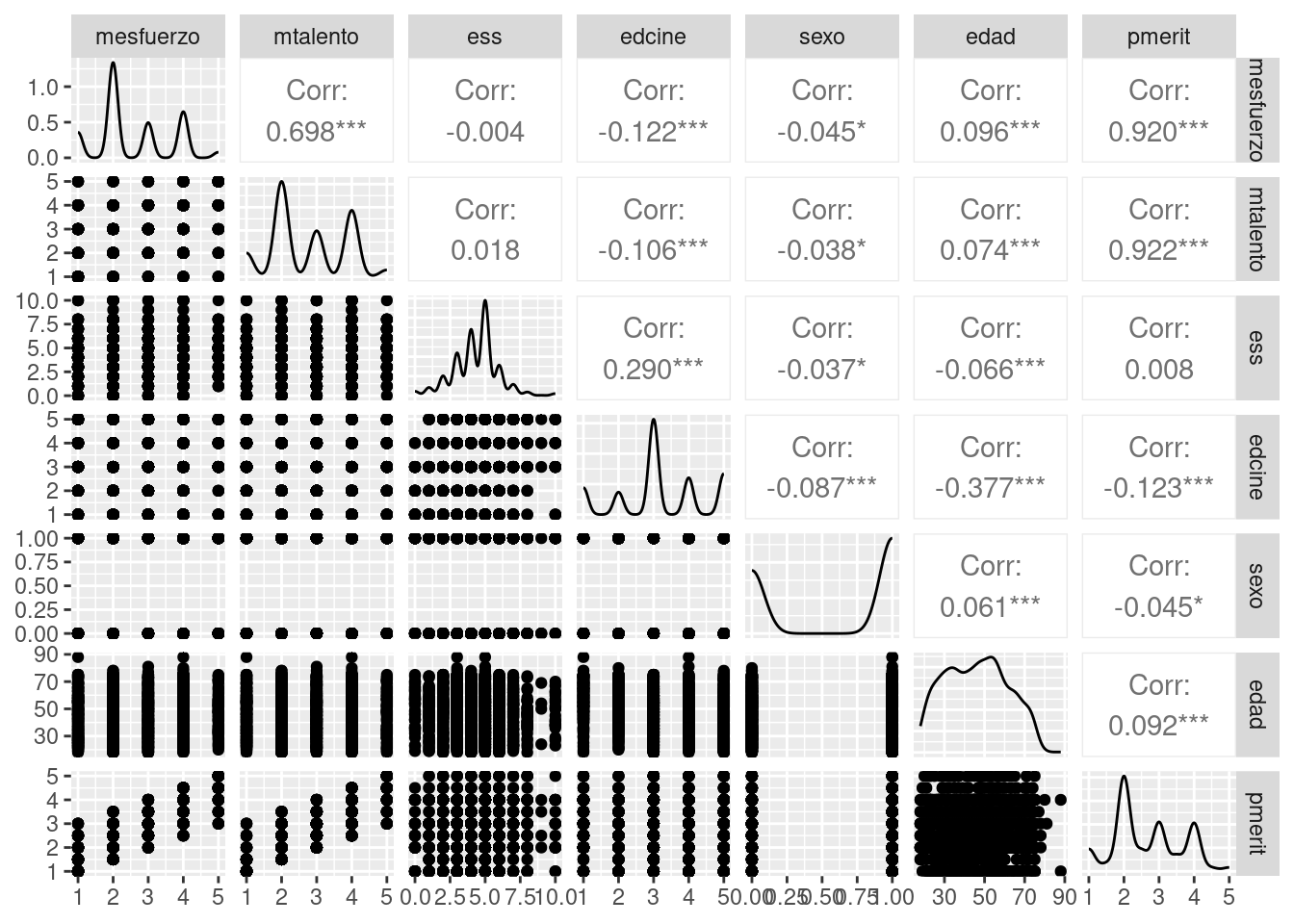

Finalmente, también se puede representar la correlación entre dos variables en un gráfico de nube de puntos o scatterplot.

sjPlot::plot_scatter(proc_elsoc, edad, ess)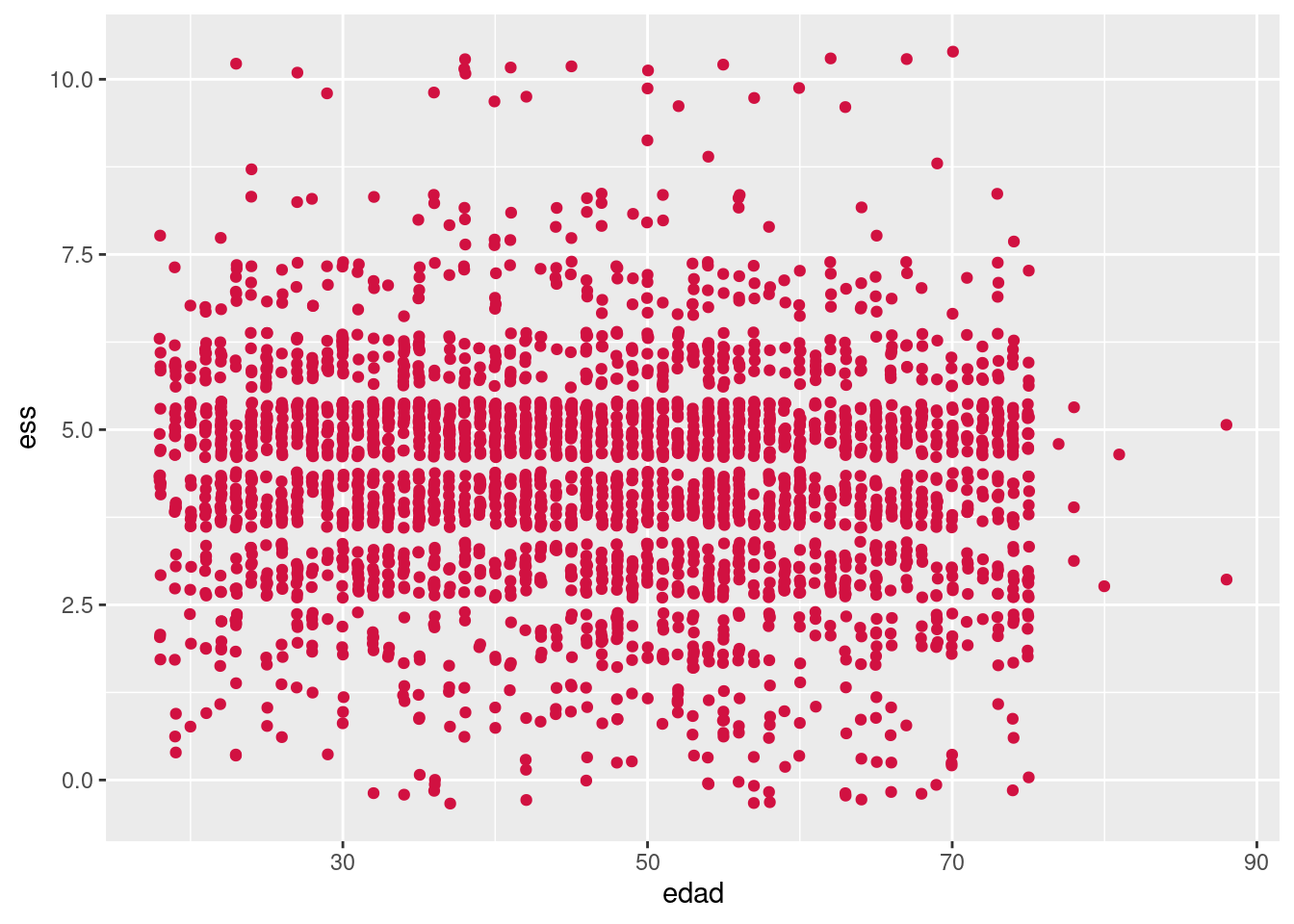

Donde:

  • cada punto representa un caso
  • la forma de la nube indica si la asociación es positiva, negativa o neutra:

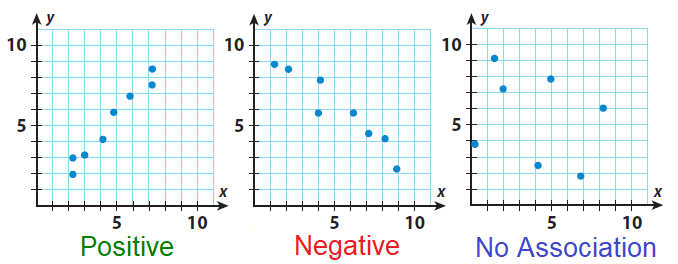
En el caso de nuestra nube de puntos entre edad y estatus social subjetivo, observamos que no hay asociación (lo que ya era indicado por su correlación de -0.07 observada en la matriz de correlaciones).

Tamaños de efecto

¿Y cómo puedo saber si el valor de la correlación es alto, medio o bajo? Si bien la correlación no nos indica causalidad, si nos permite conocer la dirección y fuerza de asociación entre dos variables. Un estándar para determinar qué tan fuerte es dicha asociación en las ciencias sociales es el propuesto por Cohen (1998).

r Significado aproximado (Cohen 1988)
< ±0.1  Muy pequeño
±0.1–0.3 Pequeño
±0.3–0.5 Moderado
>±0.5 Grande

Con estos criterios podemos interpretar de mejor manera nuestros resultados de correlación. Como se observa, mientras más alto (sea en + o -) el coeficiente, más juntos estarán los datos (puntos), mostrando un patrón.

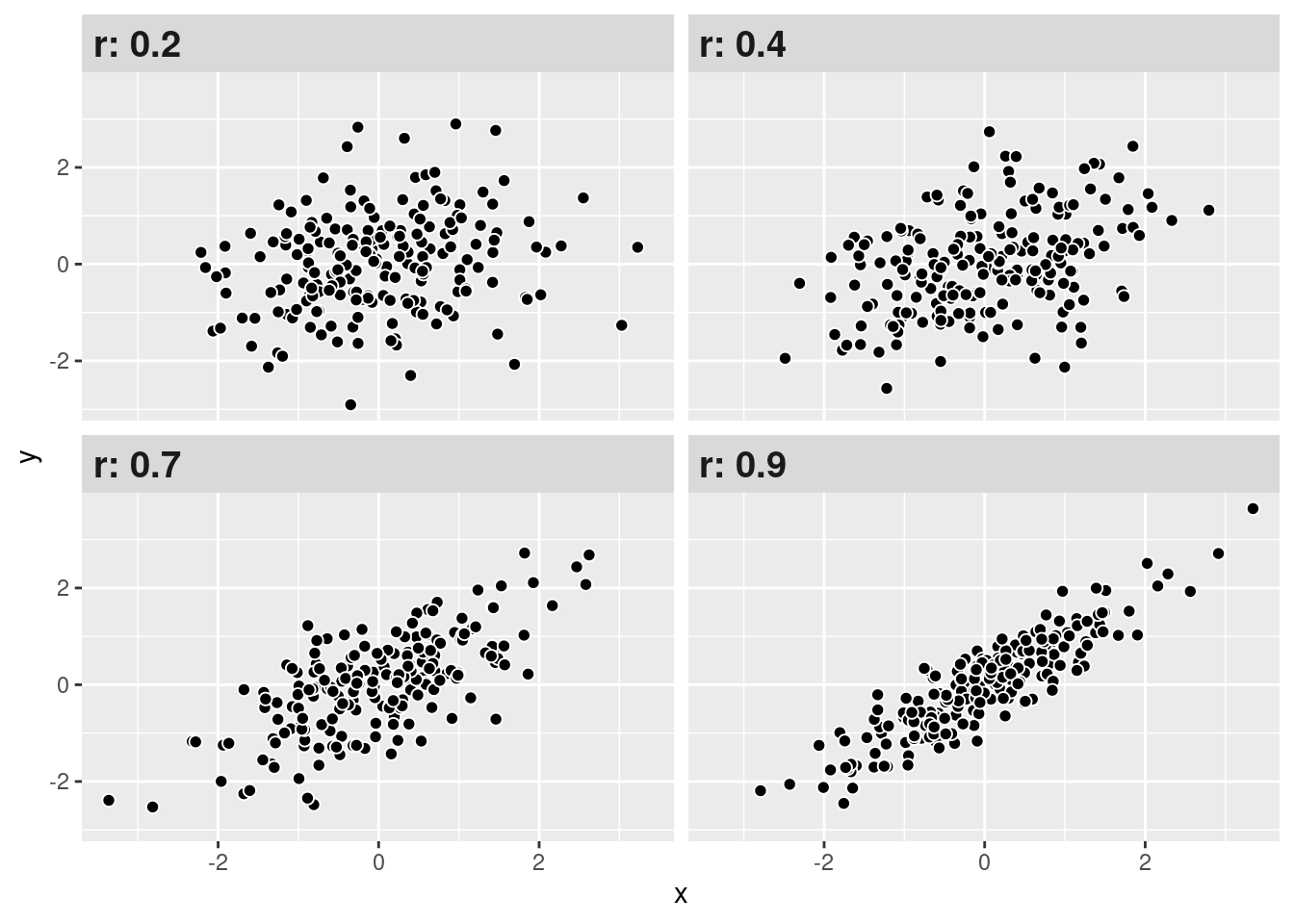
Interpretación

Recordemos nuestra matriz del comienzo:

Tenemos que la correlación entre la variable de estatus social subjetivo y años de educación es 0.3. ¿Cómo interpreto esto?

Una manera recomendable es la siguiente:

El coeficiente de correlación de Pearson entre estatus social subjetivo y años de educación es positivo y moderado (r = 0.3) según Cohen (1988).

Otros tipos de correlación: Spearman

Cuando queremos conocer la asociación entre variables que son ordinales y/o cuando nuestras variables no cumplen con los supuestos de distribución normal, podemos utilizar la correlación de Spearman.

  • El coeficiente de correlación de Spearman es una medida estadística que evalúa la relación entre variables al considerar no solo la relación lineal entre ellas, sino también su relación de orden.
  • Emplea rangos en lugar de valores numéricos para evaluar la relación.
  • Sus valores están entre -1 y 1.
  • Es alta cuando las observaciones tienen un ranking similar.

En R calcularlo es sencillo, pero debemos tener en cuenta que las variables que relacionemos tengan un orden de rango similar: por ejemplo, que el valor más bajo sea el rango más bajo y que el valor más alto sea el rango más alto.

Tomemos por ejemplo las variables mesfuerzo y mtalento.

sjmisc::frq(proc_elsoc$mesfuerzo)
x <numeric> 
# total N=2887 valid N=2887 mean=2.57 sd=1.05

Value |    N | Raw % | Valid % | Cum. %
---------------------------------------
    1 |  355 | 12.30 |   12.30 |  12.30
    2 | 1324 | 45.86 |   45.86 |  58.16
    3 |  489 | 16.94 |   16.94 |  75.10
    4 |  641 | 22.20 |   22.20 |  97.30
    5 |   78 |  2.70 |    2.70 | 100.00
 <NA> |    0 |  0.00 |    <NA> |   <NA>
sjmisc::frq(proc_elsoc$mtalento)
x <numeric> 
# total N=2887 valid N=2887 mean=2.74 sd=1.06

Value |    N | Raw % | Valid % | Cum. %
---------------------------------------
    1 |  288 |  9.98 |    9.98 |   9.98
    2 | 1155 | 40.01 |   40.01 |  49.98
    3 |  557 | 19.29 |   19.29 |  69.28
    4 |  805 | 27.88 |   27.88 |  97.16
    5 |   82 |  2.84 |    2.84 | 100.00
 <NA> |    0 |  0.00 |    <NA> |   <NA>

Ahora, calculemos el coeficiente de correlación de Spearman con cor.test.

cor.test(proc_elsoc$mesfuerzo, proc_elsoc$mtalento, method = "spearman") #especificamos metodo spearman

    Spearman's rank correlation rho

data:  proc_elsoc$mesfuerzo and proc_elsoc$mtalento
S = 1200288294, p-value < 0.00000000000000022
alternative hypothesis: true rho is not equal to 0
sample estimates:
     rho 
0.700707

Ahora conocemos el valor del coeficiente mediante al argumento rho, que es igual a 0.7, siendo positivo y grande según los criterios de Cohen (1988).

Coeficiente de determinación

El coeficiente de determinación \(R^2\) es una medida estadística que indica la proporción de la varianza total de una variable que es explicada por otra(s) variable(s). En pocas palabras,

  • se utiliza para evaluar cuánta de la variabilidad de una variable se debe a otra variable.
  • sus valores van desde 0 a 1, en donde 0 indica que ambas variables comparten el 0% de su varianza, y 1 que comparten el 100% de su varianza.

En el contexto de la correlación entre solo dos variables, el \(R^2\) es igual a elevar al cuadrado el coeficiente de correlación = (r)^2. Esto nos permite conocer qué tanto la variabilidad de una variable X estaría asociado a la variabilidad de otra variable Y.

En nuestro ejemplo anterior entre estatus social subjetivo y años de educación, teníamos que su coeficiente de correlación era r = 0.3.

coef_r <- M[4,3] # seleccionamos el coef de nuestra matriz

coef_r
[1] 0.2895925

Calculemos el \(R^2\) de esta asociación.

coef_r^2
[1] 0.0838638

Con esto, podemos decir que el 9% de la variabilidad del estatus social subjetivo es compartido con la variabilidad en los años de educación.

Resumen

Hoy aprendímos a reportar el coeficiente de correlación y cómo interpretar sus tamaños de efecto, así como también a lidiar con casos perdidos y conocer otras medidadas de correlación. En detalle, aprendímos:

  1. Cómo reportar y presentar matrices de correlación.
  2. Interpretar el tamaño de efecto de una correlación.
  3. Qué es y cómo calcular la correlación de Spearman.
  4. Tratamiento de casos perdidos.
  5. Qué es el coeficiente de determinación \(R^2\).

Reporte de progreso

Completar el reporte de progreso correspondiente a esta práctica aquí. El plazo para contestarlo es hasta el día viernes de la semana en la que se publica la práctica correspondiente.

Video de práctica

Foro